If You Could Be Earlier Than 85% of the Market?
Most read the move after it runs. The top 250K start before the bell.
Elite Trade Club turns noise into a five-minute plan—what’s moving, why it matters, and the stocks to watch now. Miss it and you chase.
Catch it and you decide.
By joining, you’ll receive Elite Trade Club emails and select partner insights. See Privacy Policy.
Elite Quant Plan – 14-Day Free Trial (This Week Only)
No card needed. Cancel anytime. Zero risk.
You get immediate access to:
Full code from every article (including today’s HMM notebook)
Private GitHub repos & templates
All premium deep dives (3–5 per month)
2 × 1-on-1 calls with me
One custom bot built/fixed for you
Try the entire Elite experience for 14 days — completely free.
→ Start your free trial now 👇
(Doors close in 7 days or when the post goes out of the spotlight — whichever comes first.)
See you on the inside.
👉 Upgrade Now →
🔔 Limited-Time Holiday Deal: 20% Off Our Complete 2026 Playbook! 🔔
Level up before the year ends!
AlgoEdge Insights: 30+ Python-Powered Trading Strategies – The Complete 2026 Playbook
30+ battle-tested algorithmic trading strategies from the AlgoEdge Insights newsletter – fully coded in Python, backtested, and ready to deploy. Your full arsenal for dominating 2026 markets.
Special Promo: Use code WINTER2025 for 20% off
Valid only until January 5, 2026 — act fast!
👇 Buy Now & Save 👇
Instant access to every strategy we've shared, plus exclusive extras.
— AlgoEdge Insights Team
Premium Members – Your Full Notebook Is Ready
The complete Google Colab notebook from today’s article (with live data, full Hidden Markov Model, interactive charts, statistics, and one-click CSV export) is waiting for you.
Preview of what you’ll get:
Inside:
The Credit Spread Options Strategy
Automating the Scanning of Credit Spreads
Implementing the Scanner in Python
Using the Scanner in Practise
Free readers – you already got the full breakdown and visuals in the article. Paid members – you get the actual tool.
Not upgraded yet? Fix that in 10 seconds here👇
Google Collab Notebook With Full Code Is Available In the End Of The Article Behind The Paywall 👇 (For Paid Subs Only)
Selling options can be a profitable avenue, if you know which spreads to sell and how to limit your risk.
Every day, 1000s of puts and calls flash attractive premiums, but either they expire worthless or blow past your risk limits when the market snaps.
Selling credit spreads looks simple. In practice, it’s a minefield: which expiry, which strikes, how wide, what credit, and how much risk is really on the table?
You need more than intuition. You need a system that ranks every possible spread by real, risk-adjusted edge.
We present a scanning system that places probability of profit, expected value, volatility, and liquidity at the center of every spread decision.
Amazon Prime members: See what you could get, no strings attached
If you spend a good amount on Amazon, do not ignore this. This card could put $100s back every year and gives you the chance to earn cash back on the purchases you already make. You could get approved extremely fast and unlock a massive welcome bonus instantly. Amazon Prime members: See what you could get, no strings attached
1. The Credit Spread Options Strategy
A credit spread combines two options: you sell one and buy another at a different strike, same type and expiry. This generates a net premium.
Why buy the second option?
Buying the further out-of-the-money option caps your risk. It creates a defined maximum loss, no matter how far the market moves against you.
Construction
Put credit spread (bull put):
Sell a put at strike K1
Buy a put at lower strike K2 (so that K2<K1)
Call credit spread (bear call):
Sell a call at strike K1
Buy a call at higher strike K2 (so that K2>K1)
Key Metrics
Net Credit (Premium Collected):

Maximum Loss (Capped):

Break-Even Price:
Puts: K1−Credit
Calls: K1+Credit
Return on Risk:

You profit if the underlying finishes above (put spread) or below (call spread) the short strike at expiry.
Losses stop at the maximum loss amount, regardless of market extremes.

Figure 1. Net payoff at expiry for two credit spread strategies: Bull Put (left): short 95 put, long 90 put, net credit $2.00. Bear Call (right): short 105 call, long 110 call, net credit $1.80. Both have capped loss and defined break-even points.
2. Automating the Scanning of Credit Spreads
You can’t manually sift through thousands of option spreads combinations and expect to consistently pick out the best one.
The market moves too fast. Most option sellers need a systematic way to surface only the most favorable trades.
The scanner works by computing the real risk, reward, and probability metrics for every liquid credit spread.
The goal is flag the small subset that offers a risk-adjusted advantage.
What makes a spread worth selling?
It’s not just the premium. You need to know the capital at risk, the odds of a win, and how that edge holds up after liquidity and volatility filters.
Core Metrics and How They Are Calculated:
Width: This is the distance between your short and long strikes.
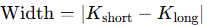
Credit: The net premium collected for selling the spread.

Max Loss: The maximum you can lose if the spread moves fully against you.

-
Break-even: The price where profit flips to loss. For puts:

Return on Risk:

Probability of Profit (POP): Approximated by delta or calculated with Black-Scholes d₂:

Expected Value (EV):

EV per Risk:

Net Vega, Net Theta: Each spread’s sensitivity to volatility and time.
You need these numbers on every possible combination, every expiry, every width.
That’s why this is a job for code, not a spreadsheet.
Here’s the workflow, step by step:
Fetch the option chain for every expiry. Pull all available puts and calls, so you don’t miss opportunities outside the front month.
Filter for liquidity and recency. Weed out stale contracts and thinly traded strikes. Focus only on spreads you could actually enter and exit.
Enrich each leg with Greeks and implied volatility. Every strike gets its own set of IV, delta, gamma, theta, vega calculated using standard models.
Construct all possible out-of-the-money credit spreads. Pair each valid short strike with a deeper OTM long strike. Compute width, credit, break-even, and all Greeks for the combined position.
Calculate edge and risk metrics for every spread.
Rank, filter, and visualize.
3. Implementing the Scanner in Python
The code below will (i) fetch live options data, (ii) enrich each strike with implied volatility and Greeks estimates, and (iii) constructs every possible out-of-the-money put or call credit spread combination.
We also calculate a robust set of risk and reward metrics for each combination. We can then sort, filter, and visualize the entire opportunity set.
3.1 Adjust Key Parameters
Set your core variables at the top. Pick your ticker, option type, expiry window, and minimum liquidity.
Each parameter is further explained as a comment in the code snippet below.
These settings filter out illiquid, stale, or mispriced options and focus the scan on real tradable spreads.
import yfinance as yf
import pandas as pd
import numpy as np
from datetime import datetime, timedelta
from math import log, sqrt, exp
from scipy.stats import norm
import plotly.express as px
import matplotlib.pyplot as plt
plt.style.use('dark_background')
# ─── PARAMETERS
TICKER = '^SPX' #"^XSP" # underlying symbol (e.g. "^XSP" or "SPY"); changing this points the scanner at a different market
OPTION_TYPE = "put" # "put" or "call"; switches between scanning put-credit spreads (OTM puts) and call-credit spreads (OTM calls)
MIN_DTE = 1 # minimum days to expiry; ↑ to avoid very short-dated (low gamma, little time decay), ↓ to include them
MAX_DTE = 90 # maximum days to expiry; ↑ to scan far-out expiries (higher extrinsic value), ↓ to focus on near-term
N_STD = 1.0 # threshold in standard deviations for a price “safety” band; ↑ widens the band (more conservative), ↓ tightens it
RISK_FREE = 0.04 # annual risk-free rate used in Black–Scholes; update to current rates—has a small effect on theoretical pricing
MIN_OI = 100 # minimum open interest; ↑ to require more liquid strikes (fewer legs), ↓ to include less-traded strikes
MIN_VOL = 20 # minimum volume today; ↑ to filter stale or inactive strikes, ↓ to accept lower-volume legs
LAST_N_DAYS = 5 # only include options last traded within this many calendar days; ↓ to require fresher trading prints, ↑ to allow older
MAX_SPREAD_PCT = 0.05 # maximum acceptable bid–ask width as a fraction of strike (e.g. 0.1 = 10%); ↓ for tighter pricing, ↑ to allow wider markets
POP_METHOD = "POP" # "delta" uses |Δ| (for calls) or 1−|Δ| (for puts) as approximate POP; "d2" uses Φ(d₂) from B–S for theoretical POP
PRICING_METHOD = "mid" # "mid" uses midpoint pricing for credit; "worst" uses bid for the short leg and ask for the long leg (more conservative)
3.2 Black-Scholes Helper Functions
We now define all pricing and Greek calculations in helper functions. We use standard Black-Scholes formulas.
These functions calculate the theoretical price of each option and extract the risk measures: delta, gamma, theta, and vega.
Each strike also gets an implied volatility estimate based on current market prices. Implied volatility is solved numerically.
These metrics essentially drive the probability, edge, and risk calculations for every spread in the scan.
# ─── BLACK–SCHOLES HELPER FUNCTIONS
def _d1(S,K,T,r,σ):
return (log(S/K)+(r+0.5*σ*σ)*T)/(σ*sqrt(T)) if (σ>0 and T>0) else np.nan
def _d2(S,K,T,r,σ):
d1 = _d1(S,K,T,r,σ)
return d1 - σ*sqrt(T) if not np.isnan(d1) else np.nan
def bs_price(S,K,T,r,σ,kind):
d1, d2 = _d1(S,K,T,r,σ), _d2(S,K,T,r,σ)
if np.isnan(d1) or np.isnan(d2):
return np.nan
if kind=="call":
return S*norm.cdf(d1) - K*exp(-r*T)*norm.cdf(d2)
else:
return K*exp(-r*T)*norm.cdf(-d2) - S*norm.cdf(-d1)
def implied_vol(mkt_price,S,K,T,r,kind):
σ = 0.2
for _ in range(60):
price = bs_price(S,K,T,r,σ,kind)
if np.isnan(price):
return np.nan
diff = price - mkt_price
if abs(diff) < 1e-6:
return max(σ,0)
d1 = _d1(S,K,T,r,σ)
vega = S * norm.pdf(d1) * sqrt(T)
if vega < 1e-8:
break
σ -= diff / vega
return np.nan
def greeks(S,K,T,r,σ,kind):
if σ<=0 or T<=0:
return np.nan, np.nan, np.nan, np.nan
d1, d2 = _d1(S,K,T,r,σ), _d2(S,K,T,r,σ)
Δ = norm.cdf(d1) if kind=="call" else norm.cdf(d1)-1
Γ = norm.pdf(d1)/(S*σ*sqrt(T))
V = S*norm.pdf(d1)*sqrt(T)*0.01
if kind=="call":
Θ = (-S*norm.pdf(d1)*σ/(2*sqrt(T))
- r*K*exp(-r*T)*norm.cdf(d2)
)/365
else:
Θ = (-S*norm.pdf(d1)*σ/(2*sqrt(T))
+ r*K*exp(-r*T)*norm.cdf(-d2)
)/365
return Δ, Γ, Θ, V3.3 Fetch Options Data and Enrich It
Pull the raw chain from yfinance. Filter for volume, open interest, and recent prints.
Compute IV, delta, gamma, theta, and vega for each strike.
Use build_spreads function to pair every valid short leg with a deeper long leg. Filter for realistic pricing.
Then, calculate credit, width, max loss, break-even, POP, EV, and Greek exposures for every spread.
# ─── FETCH & ENRICH RAW CHAIN
def load_chain(expiry_str, spot):
opt = yf.Ticker(TICKER).option_chain(expiry_str)
raw = opt.puts if OPTION_TYPE=="put" else opt.calls
raw = raw.dropna(subset=["bid","ask","strike","openInterest","volume","lastTradeDate"]).copy()
# 1) filter for recent trading (UTC‐aware)
raw["lastTradeDate"] = pd.to_datetime(raw["lastTradeDate"])
cutoff = pd.Timestamp.now(tz="UTC") - timedelta(days=LAST_N_DAYS)
raw = raw[raw["lastTradeDate"] >= cutoff]
# 2) filter out very low open interest / low volume
raw = raw[(raw.openInterest >= MIN_OI) & (raw.volume >= MIN_VOL)]
# midpoint for IV guess
raw["mid"] = (raw.bid + raw.ask) / 2
T = (datetime.strptime(expiry_str, "%Y-%m-%d") - now).days / 365
raw["iv"] = raw["delta"] = raw["gamma"] = raw["theta"] = raw["vega"] = np.nan
for i, row in raw.iterrows():
K, m = row.strike, row.mid
iv = implied_vol(m, spot, K, T, RISK_FREE, OPTION_TYPE)
Δ,Γ,Θ,V = greeks(spot, K, T, RISK_FREE, iv, OPTION_TYPE)
raw.at[i,"iv"] = iv
raw.at[i,"delta"] = Δ
raw.at[i,"gamma"] = Γ
raw.at[i,"theta"] = Θ
raw.at[i,"vega"] = V
raw["expiry"] = expiry_str
raw["DTE"] = (datetime.strptime(expiry_str, "%Y-%m-%d") - now).days
return raw.dropna(subset=["iv","delta","gamma"])
# ─── BUILD ALL CREDIT SPREADS
def build_spreads(chain, spot, threshold):
out = []
if OPTION_TYPE=="put":
shorts = chain[chain.strike < spot]
long_filter = lambda df,s: df[df.strike < s]
pop_sign = 1
else:
shorts = chain[chain.strike > spot]
long_filter = lambda df,s: df[df.strike > s]
pop_sign = -1
for _, sh in shorts.iterrows():
if (sh.ask - sh.bid)/sh.strike > MAX_SPREAD_PCT:
continue
d2 = _d2(spot, sh.strike, sh.DTE/365, RISK_FREE, sh.iv)
# choose POP method
if POP_METHOD == "delta":
pop = (1 - abs(sh.delta)) if OPTION_TYPE=="put" else sh.delta
else: # "d2"
pop = norm.cdf(pop_sign * d2)
# old POP via d2, left for reference:
# pop = norm.cdf(pop_sign * d2)
for _, lg in long_filter(chain, sh.strike).iterrows():
if (lg.ask - lg.bid)/lg.strike > MAX_SPREAD_PCT:
continue
# choose pricing method
if PRICING_METHOD == "mid":
short_price = sh.mid
long_price = lg.mid
else:
# worst-case: sell at bid, buy at ask
short_price = sh.bid if sh.bid>0 else sh.lastPrice
long_price = lg.ask if lg.ask>0 else lg.lastPrice
# old midpoint credit, left for reference:
# credit = sh.mid - lg.mid
credit = short_price - long_price
width = abs(sh.strike - lg.strike)
if credit<=0 or credit>width:
continue
max_loss = width - credit
ev = pop*credit - (1-pop)*max_loss
ev_risk = ev / max_loss
be = (sh.strike - credit) if OPTION_TYPE=="put" else (sh.strike + credit)
be_pct = abs(be - spot)/spot * 100
ev_std = ev / abs(be_pct) if be_pct else np.nan
net_vega = -sh.vega + lg.vega
net_theta = sh.theta - lg.theta
out.append({
"expiry": sh.expiry,
"DTE": sh.DTE,
"short_strike": sh.strike,
"short_price": round(short_price,3),
"short_oi": int(sh.openInterest),
"short_vol": int(sh.volume),
"long_strike": lg.strike,
"long_price": round(long_price,3),
"long_oi": int(lg.openInterest),
"long_vol": int(lg.volume),
"width": round(width,2),
"credit": round(credit,3),
"max_loss": round(max_loss,3),
"break_even": round(be,3),
"break_even_%": round(be_pct,2),
"return_on_risk": round(credit/max_loss,3),
"short_iv": round(sh.iv,3),
"long_iv": round(lg.iv,3),
"iv_skew": round(sh.iv - lg.iv,3),
"short_delta": round(sh.delta,3),
"long_delta": round(lg.delta,3),
"delta_diff": round(sh.delta - lg.delta,3),
"short_gamma": round(sh.gamma,6),
"long_gamma": round(lg.gamma,6),
"short_theta": round(sh.theta,4),
"long_theta": round(lg.theta,4),
"net_theta": round(net_theta,4),
"short_vega": round(-sh.vega,4),
"long_vega": round(lg.vega,4),
"net_vega": round(net_vega,4),
"POP": round(pop,3),
"EV": round(ev,3),
"EV_per_risk": round(ev_risk,3),
"EV_std": round(ev_std,3),
"threshold": round(threshold,2),
"below_threshold":"yes" if sh.strike < threshold else "no"
})
return out3.4 Running the Scan
Finally, we run the scannner on the entire chain across all expiries. Apply the filters. Then, build and aggregate all possible spreads.
# ─── RUN THE SCAN
now = datetime.utcnow()
spot = yf.Ticker(TICKER).history(period="1d")["Close"].iloc[-1]
all_chain, all_spreads = [], []
opt = yf.Ticker(TICKER)
for expiry in opt.options:
dte = (datetime.strptime(expiry,"%Y-%m-%d") - now).days
if not (MIN_DTE <= dte <= MAX_DTE):
continue
ch = load_chain(expiry, spot)
if ch.empty:
continue
all_chain.append(ch)
T = dte/365
atm_iv = ch.iloc[(ch.strike - spot).abs().argmin()].iv
thresh = (spot - N_STD*spot*atm_iv*sqrt(T)) if OPTION_TYPE=="put" \
else (spot + N_STD*spot*atm_iv*sqrt(T))
all_spreads += build_spreads(ch, spot, thresh)
chain = pd.concat(all_chain, ignore_index=True)
spreads = pd.DataFrame(all_spreads).sort_values("EV", ascending=False)
pd.set_option("display.float_format", lambda x: f"{x:,.4f}")
print(f"\n{TICKER} spot ${spot:,.2f} — chain rows: {len(chain)}, spreads: {len(spreads)}\n")
print(chain.head().to_string(index=False))
print("\n")
print(spreads.head(200).to_string(index=False))
Figure 2. Enriched credit spread DataFrame. Each row shows a unique OTM spread that include strikes, Greeks, IV, expected value, probability of profit, risk metrics, and liquidity filters for scanning. Dataframe is sorted by the highest EV.
3.5 Width vs EV vs DTE
Plot a 3D scatter where the x-axis is spread width, y-axis is expected value, z-axis is days to expiry. Color represents probability of profit. Bubble size reflects credit received.
This plot shows the trade-offs between risk and reward and where they cluster.
Each point represents a unique OTM credit spread. You see how expected value shifts as you vary spread width and days to expiry.
# ── filtered view, original df_plot remains unchanged
EV_FILTER = -10
df_filtered = df_plot[df_plot["EV"] >= EV_FILTER]
# ── 3D scatter with full hover_data including both strikes
fig = px.scatter_3d(
df_filtered,
x="width",
y="EV",
z="DTE",
color="POP",
size="credit",
size_max=12,
opacity=0.8,
color_continuous_scale="Viridis",
template="plotly_dark",
hover_data={
"short_strike": ":.2f", # short put strike
"long_strike": ":.2f", # long put strike
"credit": ":.3f", # credit received
"POP": ":.1%", # probability of profit
"EV": ":.3f", # expected value
"EV_per_risk": ":.3f", # EV / max_loss
"DTE": True # days to expiry
}
)
fig.update_layout(
title=f"3D Scatter: Width vs EV vs DTE (EV ≥ {EV_FILTER}), Sized by Credit",
scene=dict(
xaxis_title="Spread Width",
yaxis_title="Expected Value (EV)",
zaxis_title="Days to Expiry (DTE)"
),
margin=dict(l=0, r=0, b=0, t=50)
)
fig.show()
Figure 2. Interactive 3D scatterplot of OTM credit spreads. X-axis shows spread width, Y-axis shows expected value, Z-axis is days to expiry. Color reflects probability of profit; bubble size tracks credit received.
The color gradient shows days to expiry (DTE), from short-term (purple) to long-term (yellow).
You see a downward slope. As spread width increases, expected value drops further negative.
Wider spreads collect more premium, but risk much larger losses, so the average expected outcome deteriorates fast.
The color pattern shows that longer-dated spreads tend to stack toward the right, as far-expiry options allow for wider strikes and larger payouts.
However, the EV for these wide, far-dated spreads is still negative, and sharply so.
This is the intuition: more time and distance from the money increases the premium, but the odds of a bad loss also climb.
Therefore, most spreads remain negative EV because markets efficiently price risk into the options chain.
3.6 EV per Risk By DTE Bucket
Bucket spreads by days to expiry. Plot a violin for EV_per_risk in each 5-day DTE group.
Each violin displays the distribution of EV per risk within a 5-day expiry bucket.
You spot which timeframes offer better reward for risk and identify where outliers or unusually high edges cluster.
# ── build 5-day buckets
step = 5
df_violin = df_plot.copy()
max_dte = int(np.ceil(df_violin["DTE"].max() / step) * step)
bins = list(range(0, max_dte + step, step))
labels = [f"{b}-{b+step}" for b in bins[:-1]]
df_violin["DTE_bucket"] = pd.cut(
df_violin["DTE"],
bins=bins,
labels=labels,
right=False
)
# ── keep only rows that actually landed in a bucket
df_violin = df_violin.dropna(subset=["DTE_bucket", "EV_per_risk"])
# remove empty categories and capture the ones that remain
df_violin["DTE_bucket"] = df_violin["DTE_bucket"].cat.remove_unused_categories()
bucket_order = df_violin["DTE_bucket"].cat.categories.tolist()
# ── violin plot in ascending DTE order
fig = px.violin(
df_violin,
x="DTE_bucket",
y="EV_per_risk",
box=True,
points=False,
category_orders={"DTE_bucket": bucket_order}, # ascending & no empty bins
template="plotly_dark"
)
fig.update_layout(
title="EV per Risk by 5-Day DTE Buckets",
xaxis_title="Days to Expiry (ascending buckets)",
yaxis_title="EV per Risk",
showlegend=False,
margin=dict(l=40, r=40, b=40, t=60)
)
fig.show()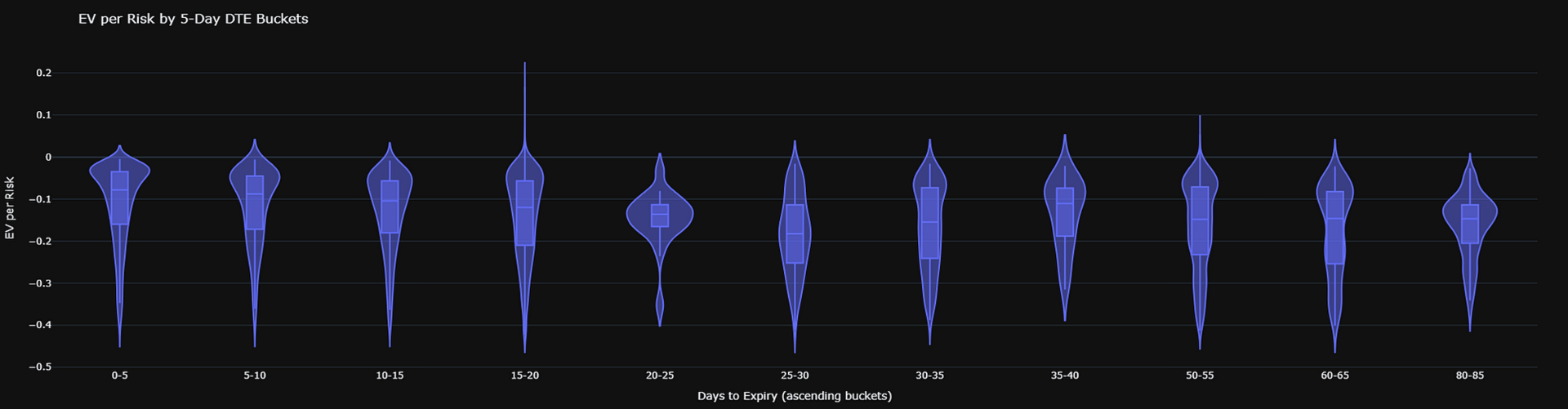
Figure 3. Distribution of risk-adjusted edge (EV per risk) for each 5-day DTE bucket. Each violin shows how EV/risk varies across time-to-expiry.
3.7 EV per Risk By Strike vs. DTE
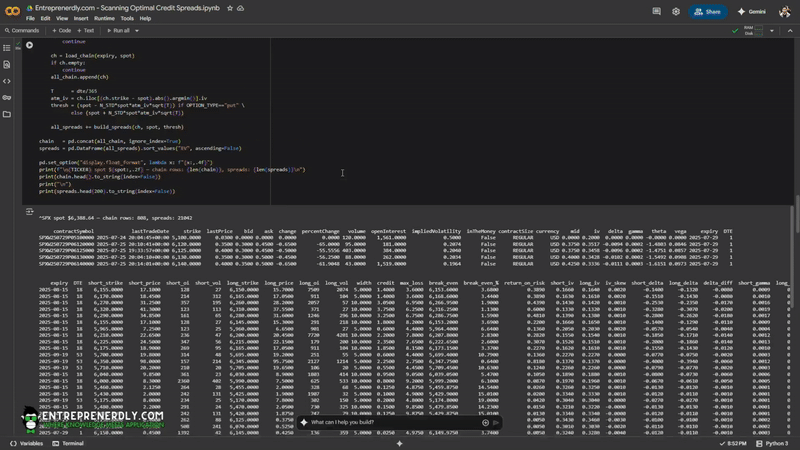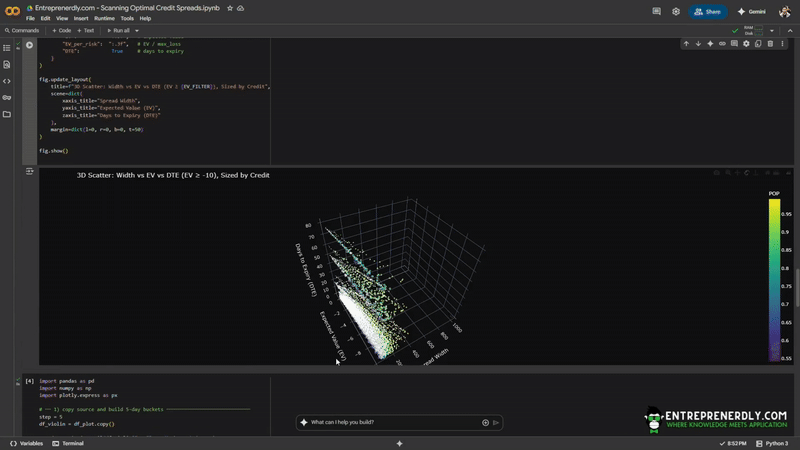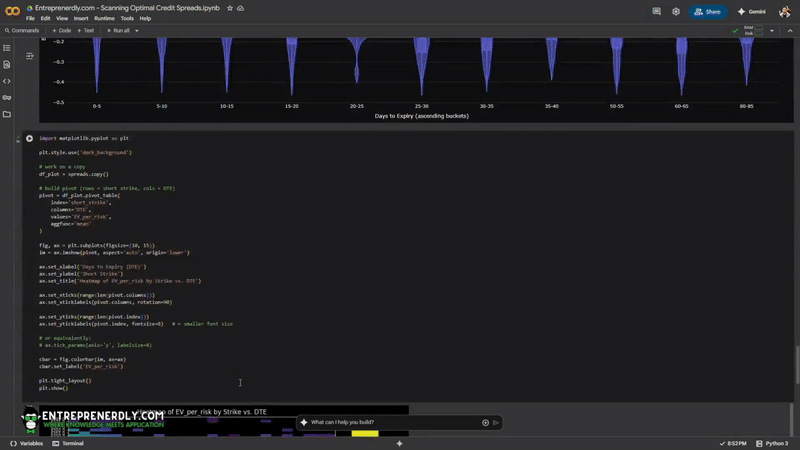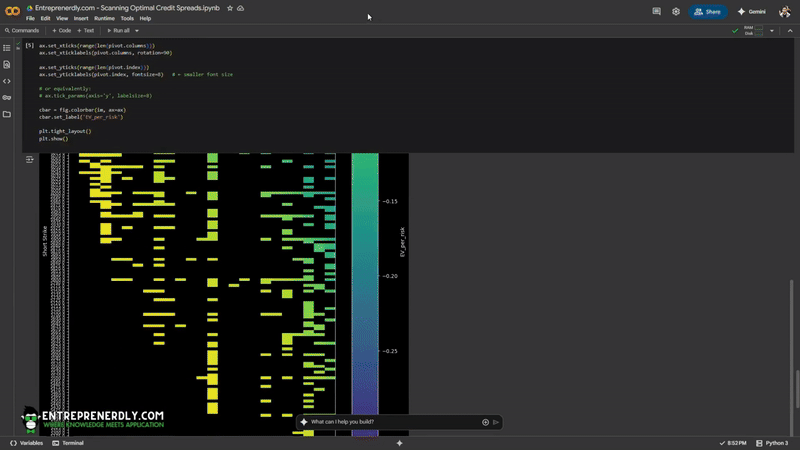
Pivot to a heatmap where the y-axis is short strike and x-axis is DTE. Color shows average EV_per_risk for each combination.
This heatmap highlights where the most attractive credit spreads concentrate across strikes and expiries.
Brighter regions signal strike/DTE pairs with higher average risk-adjusted edge.
# work on a copy
df_plot = spreads.copy()
# build pivot (rows = short strike, cols = DTE)
pivot = df_plot.pivot_table(
index='short_strike',
columns='DTE',
values='EV_per_risk',
aggfunc='mean'
)
fig, ax = plt.subplots(figsize=(10, 15))
im = ax.imshow(pivot, aspect='auto', origin='lower')
ax.set_xlabel('Days to Expiry (DTE)')
ax.set_ylabel('Short Strike')
ax.set_title('Heatmap of EV_per_risk by Strike vs. DTE')
ax.set_xticks(range(len(pivot.columns)))
ax.set_xticklabels(pivot.columns, rotation=90)
ax.set_yticks(range(len(pivot.index)))
ax.set_yticklabels(pivot.index, fontsize=8) # ← smaller font size
# or equivalently:
# ax.tick_params(axis='y', labelsize=8)
cbar = fig.colorbar(im, ax=ax)
cbar.set_label('EV_per_risk')
plt.tight_layout()
plt.show()
Figure 4. Heatmap of EV per risk by short strike and DTE. Brighter regions show strike/expiry pairs with higher normalized edge.
4. Using the Scanner in Practise
Most OTM credit spreads show negative expected value after filtering for liquidity and realistic fills.
This should not surprise anyone who has traded options. The options market remains highly efficient.
Market makers and smart money price risk into the contracts. Spreads with fat positive EV rarely pass through real-world filters.
Yet, the scanner gives spread sellers practical tools to improve. You can:
Rank spreads by EV_per_risk to normalize edge by dollars at risk. This helps size trades and avoid overexposing capital to low-probability outliers.
Screen for above-median POP to favor probability over payout, especially if you want a smoother P&L.
Apply a strict DTE window to reduce event risk or focus on premium decay. The plots make it clear: edge varies with time-to-expiry.
Filter by open interest and volume to avoid slippage and assignment risk. The most attractive theoretical spreads are often not tradeable in size.
Sort by IV skew and Greek exposures to avoid hidden risks, especially in volatile or one-sided markets.
5. Limitations and Extensions
5.1 Limitations
The scan does not include commissions, taxes, or execution friction. Fill prices can slip below theoretical marks, especially in wide or illiquid markets.
Probability estimates rely on Black-Scholes and delta, which assume log-normal returns and constant volatility. This model does not capture real-world jumps, volatility skew, or correlation breakdowns during market stress. Event risk and earnings are not filtered out.
The code does not account for early assignment or margin requirements, both of which can affect outcomes for real accounts. It does not filter for dividends, hard-to-borrow conditions, or regulatory constraints.
5.2 Extensions
Extensions are straightforward. You can plug in alternate pricing models, add earnings and macro filters, or re-rank spreads by custom criteria such as short-term realized volatility.
You can also backtest realized outcomes against historical data to validate the edge, or automate execution by integrating with broker APIs.
Use the scanner as a research tool, not a trading system. It helps clarify where the market offers potential edge and where efficient pricing leaves little room for profit.
Concluding Thoughts
Most edge in option selling comes from systematically avoiding the worst trades.
That discipline alone is an edge in a market built to exploit shortcuts and wishful thinking.
Subscribe to our premium content to read the rest.
Become a paying subscriber to get access to this post and other subscriber-only content.
Upgrade