
Fuel your business brain. No caffeine needed.
Consider this your wake-up call.
Morning Brew}} is the free daily newsletter that powers you up with business news you’ll actually enjoy reading. It’s already trusted by over 4 million people who like their news with a bit more personality, pizazz — and a few games thrown in. Some even come for the crosswords and quizzes, but leave knowing more about the business world than they expected.
Quick, witty, and delivered first thing in the morning, Morning Brew takes less time to read than brewing your coffee — and gives your business brain the boost it needs to stay sharp and in the know.
Elite Quant Plan – 14-Day Free Trial (This Week Only)
No card needed. Cancel anytime. Zero risk.
You get immediate access to:
Full code from every article (including today’s HMM notebook)
Private GitHub repos & templates
All premium deep dives (3–5 per month)
2 × 1-on-1 calls with me
One custom bot built/fixed for you
Try the entire Elite experience for 14 days — completely free.
→ Start your free trial now 👇
(Doors close in 7 days or when the post goes out of the spotlight — whichever comes first.)
See you on the inside.
👉 Upgrade Now →
🔔 Limited-Time Holiday Deal: 20% Off Our Complete 2026 Playbook! 🔔
Level up before the year ends!
AlgoEdge Insights: 30+ Python-Powered Trading Strategies – The Complete 2026 Playbook
30+ battle-tested algorithmic trading strategies from the AlgoEdge Insights newsletter – fully coded in Python, backtested, and ready to deploy. Your full arsenal for dominating 2026 markets.
Special Promo: Use code WINTER2025 for 20% off
Valid only until December 31, 2025 — act fast!
👇 Buy Now & Save 👇
Instant access to every strategy we've shared, plus exclusive extras.
— AlgoEdge Insights Team
Premium Members – Your Full Notebook Is Ready
The complete Google Colab notebook from today’s article (with live data, full Hidden Markov Model, interactive charts, statistics, and one-click CSV export) is waiting for you.
Preview of what you’ll get:

Inside this single-cell Google Colab code:
Automatic SPY data download (from 2020 → today) using yfinance
EWMA + shrinkage adaptive drift estimation (blends recent market returns with risk-free rate)
Real-time ATM implied volatility pulled from SPY options chain (nearest expiration)
Analytical log-normal GBM forecast (no Monte Carlo needed)
Probabilistic price bands at 68%, 80%, 90% confidence levels
Asymmetric upside/downside bands (true log-normal property)
Console summary with current price, IV, drift, and 100-day forecast ranges
Ready to change ticker (e.g. AAPL, BTC-USD, QQQ) in one line
Uses only standard libraries (numpy, pandas, yfinance, scipy, matplotlib) – no extra installs needed beyond yfinance
Free readers – you already got the full breakdown and visuals in the article. Paid members – you get the actual tool.
Not upgraded yet? Fix that in 10 seconds here👇
Google Collab Notebook With Full Code Is Available In the End Of The Article Behind The Paywall 👇 (For Paid Subs Only)
With just historical returns and option-implied volatility, you can model realistic price bands using ‘Geometric Brownian Motion’.
GBM lets us generate forward-looking price scenarios that reflect both time-varying uncertainty and the compounding nature of asset returns.
Here, we’ll build a probabilistic forecast model for SPY which integrates market-based volatility with adaptive drift to simulate confidence intervals.
The complete Python notebook for the analysis is provided below.

1. GBM for Price Forecasting
GBM is useful because it balances simplicity with theoretical soundness when modeling future price distributions.
The method assumes that asset prices follow a log-normal process, meaning the logarithm of the price evolves as a Wiener process with a drift.
What investment is rudimentary for billionaires but ‘revolutionary’ for 70,571+ investors entering 2026?
Imagine this. You open your phone to an alert. It says, “you spent $236,000,000 more this month than you did last month.”
If you were the top bidder at Sotheby’s fall auctions, it could be reality.
Sounds crazy, right? But when the ultra-wealthy spend staggering amounts on blue-chip art, it’s not just for decoration.
The scarcity of these treasured artworks has helped drive their prices, in exceptional cases, to thin-air heights, without moving in lockstep with other asset classes.
The contemporary and post war segments have even outpaced the S&P 500 overall since 1995.*
Now, over 70,000 people have invested $1.2 billion+ across 500 iconic artworks featuring Banksy, Basquiat, Picasso, and more.
How? You don’t need Medici money to invest in multimillion dollar artworks with Masterworks.
Thousands of members have gotten annualized net returns like 14.6%, 17.6%, and 17.8% from 26 sales to date.
*Based on Masterworks data. Past performance is not indicative of future returns. Important Reg A disclosures: masterworks.com/cd
This is a foundational assumption in option pricing theory, most notably in the Black-Scholes model.
In the context of forecasting, it allows us to generate forward price scenarios that incorporate both compounding returns and increasing uncertainty over time.

St is the asset price at time t
μ is the drift term (expected return)
σ is the volatility (standard deviation of returns)
Wt is a Wiener process (standard Brownian motion)
Solving this stochastic differential equation gives the following form for simulating future prices:
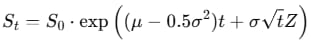
Here, S0 is the current price, and Z∼N(0,1) is a standard normal random variable.
The model has two key inputs:
1. Drift (μ): expected rate of return (average directional movement).
2. Volatility (σ): reflects the expected variability or risk.
In practice, we’ll estimate the drift using a smoothed version of historical returns and combine it with the risk-free rate using a shrinkage approach.
For volatility, we’ll use ATM implied volatility from SPY options as a market-implied measure of future uncertainty, rather than relying on historical variance.
Since implied volatility often overestimates future realized volatility, the resulting forecasts tend to be wider, more conservative and risk aware.
2. Price Data and Parameters
To build a forward-looking price forecast, we need two things: (i) historical data to estimate drift, and (ii) parameter settings to control the simulation.
We’ll use daily closing prices for SPY. Data is pulled from Yahoo Finance from January 1, 2020, to June 15, 2025 as an example.
This 5 year window provides a sufficiently rich sample to compute stable return estimates, but still keep the model responsive to recent trends.
The functionality of each parameter is defined below.
import numpy as np
import pandas as pd
import yfinance as yf
from scipy.stats import norm
import matplotlib.pyplot as plt
# Parameters
TICKER = 'SPY' # Ticker symbol for the asset (can be changed to any tradable equity or ETF)
START = '2020-01-01' # Start date for historical price data
END = '2025-06-15' # End date for historical price data
INTERVAL = '1d' # Price data frequency; use '1d' for daily returns (works best for GBM modeling)
LEN = 100 # Span for EWMA drift estimation; higher = smoother trend, lower = more sensitivity to recent changes
SMOOTH_LEN = 20 # Placeholder for optional smoothing (not used); can be repurposed for volatility smoothing
FORECAST_LEN = 100 # Number of trading days to forecast; longer = wider bands, more uncertainty in projections
CONF_LEVELS = [68, 80, 90] # Confidence intervals; increasing these adds wider bounds to capture more extreme outcomes
SHRINK_WEIGHT = 0.8 # Blend weight for EWMA drift vs. risk-free rate; closer to 1 = follow market trend, closer to 0 = conservative baseline
RISK_FREE_RATE = 0.04 # Annualized risk-free rate; used as a stabilizer for drift and anchor when returns are volatile or unreliableFrom the price series, we calculate daily log returns, defined as:

Log returns are additive over time and align with the continuous compounding assumption used in GBM.
# Download historical data
df = yf.download(
TICKER, start=START, end=END,
interval=INTERVAL,
auto_adjust=True, progress=False, threads=False
)
if isinstance(df.columns, pd.MultiIndex):
df.columns = df.columns.get_level_values(0)
# Log returns
daily_ret = np.log(df['Close'] / df['Close'].shift(1)).dropna()3. Estimating Drift Using EWMA and Shrinkage
In the GBM model, the drift term μ represents the directional component of price evolution, i.e. the part that determines whether prices tend to rise, fall, or stay flat over time.
A simple estimate of drift would be the average of historical log returns. But this has two problems:
It treats old returns as equally important as recent ones.
It’s noisy and unstable over short lookback periods.
Instead, we use an Exponentially Weighted Moving Average of log returns.
This gives more weight to recent data while and still capture longer-term trends. The EWMA drift is computed recursively using:

Where:
rt−1 is the most recent log return
μEWMA,t−1 is the previous EWMA estimate
α=2/(span+1) is the smoothing factor derived from the span
The span parameter controls sensitivity.
A larger span produces a smoother, more stable trend. A smaller span reacts faster to recent market moves but can overfit short-term noise.
Even so, relying solely on past returns can be risky, especially when markets mean-revert or shift regimes.
To stabilize our estimate, we apply shrinkage toward the daily risk-free rate, calculated as:

We combine the two using a shrinkage weight w:

This lets us balance responsiveness with robustness.
When w=1, we fully trust historical returns. When w=0, we default to the neutral baseline.
A value like w=0.8 leans toward adaptive behavior and still stay grounded.
# EWMA drift estimate
drift_ewma = daily_ret.ewm(span=LEN, adjust=False).mean().iloc[-1]
rf_daily = RISK_FREE_RATE / 252
drift = SHRINK_WEIGHT * drift_ewma + (1 - SHRINK_WEIGHT) * rf_daily4. Getting Implied Volatility from Options Data
Volatility is the second core input in the GBM model. It controls the width of the forecast distribution, i.e. how far prices are expected to deviate from the drift path.
There are two main ways to estimate volatility: using historical data (realized volatility) or using market pricing (implied volatility).
RV is backward-looking. It’s calculated from past returns and reflects how volatile the asset has been.
IV, on the other hand, is derived from the prices of traded options. It reflects the market’s consensus expectation of future volatility.
In this model, we use ATM (at-the-money) implied volatility from SPY options with the nearest expiration date.
ATM options are highly liquid and most sensitive to volatility. This makes them ideal for extracting a clean estimate.
Programatically, we identify the strike price closest to the current spot price and extract its IV.
Since option IV is annualized, we convert it to a daily scale to match the GBM time steps:
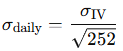
Please note again that using IV instead of RV results in wider forecast bands, because IV tends to overstate actual volatility.
# Fetch ATM implied volatility
ticker_obj = yf.Ticker(TICKER)
expirations = ticker_obj.options
if not expirations:
raise RuntimeError('No option expirations found')
exp = expirations[0]
opt_chain = ticker_obj.option_chain(exp)
calls = opt_chain.calls
a = df['Close'].iloc[-1]
atm_idx = (calls['strike'] - a).abs().idxmin()
iv = calls.loc[atm_idx, 'impliedVolatility']
sigma = iv / np.sqrt(252)5. Simulating Price Paths with GBM
We can now simulate forward prices using the GBM model.
Instead of only simulating random paths, we directly compute key quantiles of the distribution.
At each future time step t, we compute the following:
Median forecast (50th percentile):

Lower bound at confidence level c:

Upper bound at confidence level c:
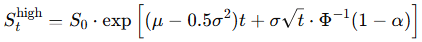
α=(1−c)/2 for a given confidence level (e.g. 90%)
Φ−1 is the inverse CDF of the standard normal distribution
This approach produces price bands that grow wider over time to capture the compounding effect of volatility.
The forecasts are skewed right due to the log-normal structure, which reflects the fact that prices can rise more than they can fall.
# Forecast dates + extra padding for annotations
last_date = df.index[-1]
dates = pd.date_range(
start=last_date + pd.Timedelta(days=1),
periods=FORECAST_LEN + 10, # add 10 days for spacing
freq='B'
)
forecast_dates = dates[:FORECAST_LEN]
# Forecast
S0 = df['Close'].iloc[-1]
d = {f'Low{lvl}': [] for lvl in CONF_LEVELS}
for lvl in CONF_LEVELS:
d[f'High{lvl}'] = []
d['Median'] = []
for i in range(1, FORECAST_LEN + 1):
mu_t = (drift - 0.5 * sigma**2) * i
vol_t = sigma * np.sqrt(i)
d['Median'].append(S0 * np.exp(mu_t + vol_t * norm.ppf(0.5)))
for lvl in CONF_LEVELS:
alpha = (1 - lvl / 100) / 2
low = S0 * np.exp(mu_t + vol_t * norm.ppf(alpha))
high = S0 * np.exp(mu_t + vol_t * norm.ppf(1 - alpha))
d[f'Low{lvl}'].append(low)
d[f'High{lvl}'].append(high)
forecast_df = pd.DataFrame(d, index=forecast_dates)6. Visualizing Forecast Bands
Finally, we overlay the projected price bands on the historical price series.
The median forecast path is plotted alongside upper and lower bounds at each confidence level. We annotate the final-day values for each.
# Plot
plt.style.use('dark_background')
plt.figure(figsize=(10, 6))
plt.plot(df['Close'], label='Historical Close')
plt.plot(forecast_df['Median'], '--', label='Median')
for lvl in CONF_LEVELS:
plt.plot(forecast_df[f'Low{lvl}'], label=f'{lvl}% Band')
plt.plot(forecast_df[f'High{lvl}'])
plt.legend()
plt.title(
f'GBM Log-Normal Forecast with IV & Drift Shrinkage for {TICKER} '
f'[{round(iv * 100, 1)}% IV, {FORECAST_LEN}d Horizon]'
)
plt.xlabel('Date')
plt.ylabel('Price')
# Annotations
last_idx = forecast_df.index[-1]
for lvl in CONF_LEVELS:
for pref in ['Low', 'High']:
val = forecast_df[f'{pref}{lvl}'].iloc[-1]
plt.annotate(f'{pref}{lvl}: {val:.2f}', xy=(last_idx, val),
xytext=(5, 0), textcoords='offset points', fontsize=8)
med_val = forecast_df['Median'].iloc[-1]
plt.annotate(f'Median: {med_val:.2f}', xy=(last_idx, med_val),
xytext=(5, 10), textcoords='offset points', fontsize=8)
plt.xlim(df.index[0], last_idx + pd.Timedelta(days=10))
plt.show()
Figure 1. Probabilistic forecast of SPY using GBM with implied volatility and EWMA-based drift. Bands represent 68%, 80%, and 90% confidence intervals over a 100-day trading horizon.
The forecast bands give a probabilistic envelope for where SPY may trade over the next 100 trading days.
The median path is the expected price trajectory based on the blended drift estimate, while the upper and lower bounds represent uncertainty intervals at 68%, 80%, and 90% confidence levels.
Several insights:
The forecast is asymmetric, i.e. upside potential is more open-ended than downside, consistent with the log-normal distribution in GBM.
The width of the bands expands over time which reflects compounding volatility and increasing uncertainty.
The use of IV results in wide forecast bands. This is intentional: IV tends to produce conservative, risk-aware projections.
7. Limitations
The model comes with limitations:
It assumes constant volatility and drift over the forecast horizon. In reality, both can shift abruptly.
GBM does not account for fat tails or jumps. It underrepresents the probability of extreme events (e.g. crashes or rallies).
The IV is single-expiration and ATM only. A fuller term structure or smile-adjusted volatility surface would yield more nuanced projections.
Concluding Thoughts
Forecasts don’t need to be point guesses. Forecasts can been seen as a range of what’s reasonable and preparing accordingly.
Subscribe to our premium content to read the rest.
Become a paying subscriber to get access to this post and other subscriber-only content.
Upgrade






