
If you work in fintech or finance, you already have too many tabs open and not enough time.
Fintech Takes is the free newsletter senior leaders actually read. Each week, we break down the trends, deals, and regulatory moves shaping the industry — and explain why they matter — in plain English.
No filler, no PR spin, and no “insights” you already saw on LinkedIn eight times this week. Just clear analysis and the occasional bad joke to make it go down easier.
Get context you can actually use. Subscribe free and see what’s coming before everyone else.
Elite Quant Plan – 14-Day Free Trial (This Week Only)
No card needed. Cancel anytime. Zero risk.
You get immediate access to:
Full code from every article (including today’s HMM notebook)
Private GitHub repos & templates
All premium deep dives (3–5 per month)
2 × 1-on-1 calls with me
One custom bot built/fixed for you
Try the entire Elite experience for 14 days — completely free.
→ Start your free trial now 👇
(Doors close in 7 days or when the post goes out of the spotlight — whichever comes first.)
See you on the inside.
👉 Upgrade Now →
🔔 Limited-Time Holiday Deal: 20% Off Our Complete 2026 Playbook! 🔔
Level up before the year ends!
AlgoEdge Insights: 30+ Python-Powered Trading Strategies – The Complete 2026 Playbook
30+ battle-tested algorithmic trading strategies from the AlgoEdge Insights newsletter – fully coded in Python, backtested, and ready to deploy. Your full arsenal for dominating 2026 markets.
Special Promo: Use code DECEMBER2025 for 20% off
Valid only until December 20, 2025 — act fast!
👇 Buy Now & Save 👇
Instant access to every strategy we've shared, plus exclusive extras.
— AlgoEdge Insights Team
Premium Members – Your Full Notebook Is Ready
The complete Google Colab notebook from today’s article (with live data, full Hidden Markov Model, interactive charts, statistics, and one-click CSV export) is waiting for you.
Preview of what you’ll get:

Inside:
Automatic gold data download (2008 → today)
Real 3-state Gaussian HMM for volatility regimes
Beautiful interactive Plotly charts
Regime duration & performance tables
Ready-to-use CSV export
Bonus: works on Bitcoin, SPX, or any ticker with one line change
Free readers – you already got the full breakdown and visuals in the article. Paid members – you get the actual tool.
Not upgraded yet? Fix that in 10 seconds here👇
Google Collab Notebook With Full Code Is Available In the End Of The Article Behind The Paywall 👇 (For Paid Subs Only)
Previously, we showed how Dynamic Time Warping (DTW) could be used in identifying recurring price patterns in stock data, and how to leverage these patterns for predictive purposes.
However, price alone might not provide a sufficient view of current market conditions. In this article, we augment the idea of our pattern recognition framework with additional variables, providing a richer representation of market dynamics.
The core of the pattern recognition method still relies on DTW but with a twist. Instead of just comparing the price data, we now also compare the technical indicators data between different windows.
To efficiently manage the computational complexity and to distill the essence of these indicators, we employ Principal Component Analysis to reduce the dimensionality of the indicators data into a manageable set of uncorrelated variables.
1. Methodology — PCA + DTW
The method combines PCA and DTW to not only find patterns purely related to price but to also bring technical indicators into the mix for a more comprehensive technique.
First, we’ll very briefly go over each technique on its own, i.e. PCA and DTW, and then explore how they come together in the framework to help identify patterns in stock price data.
Go from AI overwhelmed to AI savvy professional
AI will eliminate 300 million jobs in the next 5 years.
Yours doesn't have to be one of them.
Here's how to future-proof your career:
Join the Superhuman AI newsletter - read by 1M+ professionals
Learn AI skills in 3 mins a day
Become the AI expert on your team
1.1 Principal Component Analysis
PCA is a statistical technique used for dimensionality reduction, which is very valuable when navigating through a high-dimensional space of data, in this case, technical indicators.
It works by identifying the “principal components” that capture the most variance within the data, thus encapsulating the essential information in a reduced-dimensional space.
One way to think about PCA is that it helps to reduce the number of variables into a few variables that capture most of the variance and are uncorrelated with one another.
We will not dive too much into the inner workings of PCA, but there is a wealth of material available online for those interested in a deeper understanding.
1.2 Dynamic Time Warping
DTW is a method used for measuring the similarity between two temporal sequences, i.e. time series, which may vary in length. DTW aligns sequences in a time-warped manner, allowing for a more nuanced comparison. The DTW distance formula is given by

The DTW distance between two time series A and B of potentially unequal length. ai and bj(i) denote the elements of A and B at arbitrary indices i and j(i) respectively. DTW allows for optimal alignment between the points of the two time series, thereby enabling a more flexible measure of similarity.
In our context, it serves as a tool for comparing price movements over specific time frames. And the methodology could be expanded even when the price movements are of differing lengths.
1.3 Pattern Recognition Method
The aim is to identify patterns in a designated “current window” of price data by comparing it with numerous “past windows” from the historical data. These windows encapsulate a specified number of days, and the process is iterated for different window sizes to identify patterns across various time frames.
For each window, a dual comparison is performed using DTW. One comparison is on the price data while the other is on the PCA-reduced technical indicators data. We compute composite distance measure for each past window vis-a-vis the current window, factoring in both the price data and the technical indicators data.
1.4 Weighting Scheme: PCA vs DTW
We introduce a weight parameter to serve as a fulcrum, balancing the emphasis between the price data and the technical indicators data. By tweaking this parameter, the methodology can be tuned to lean more toward either of the two data sources.

The formula shows the weighted distance computation, where D is the combined DTW distance, Dreturns and Dindicators are the DTW distances from percentage change and PCA Reduced indicator features respectively, and ω is the weighting factor.
1.5 Mining Patterns in the Historical Data
The objective is to identify past windows that exhibit a low composite distance to the current window, indicating a high degree of similarity. The lower the distance, the more analogous the patterns.
The three to five most similar past windows are then retrieved and visualized, and their subsequent price movements are analyzed to project a median subsequent price path for the current window.
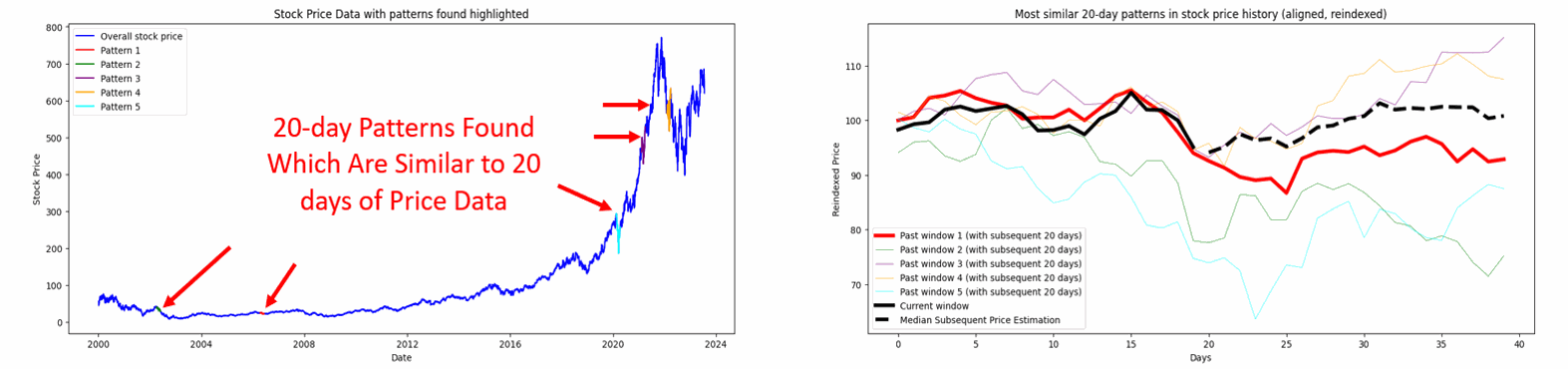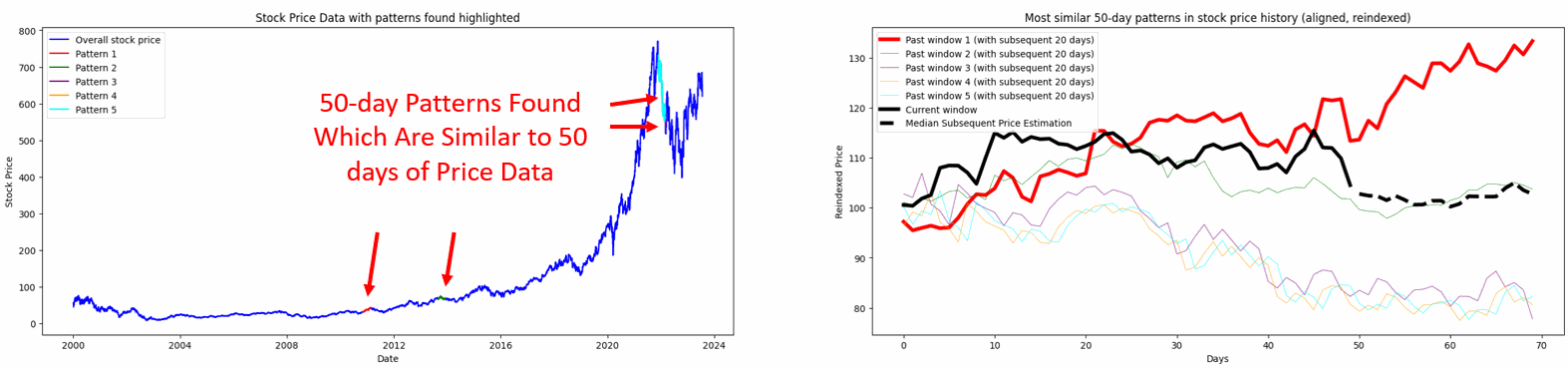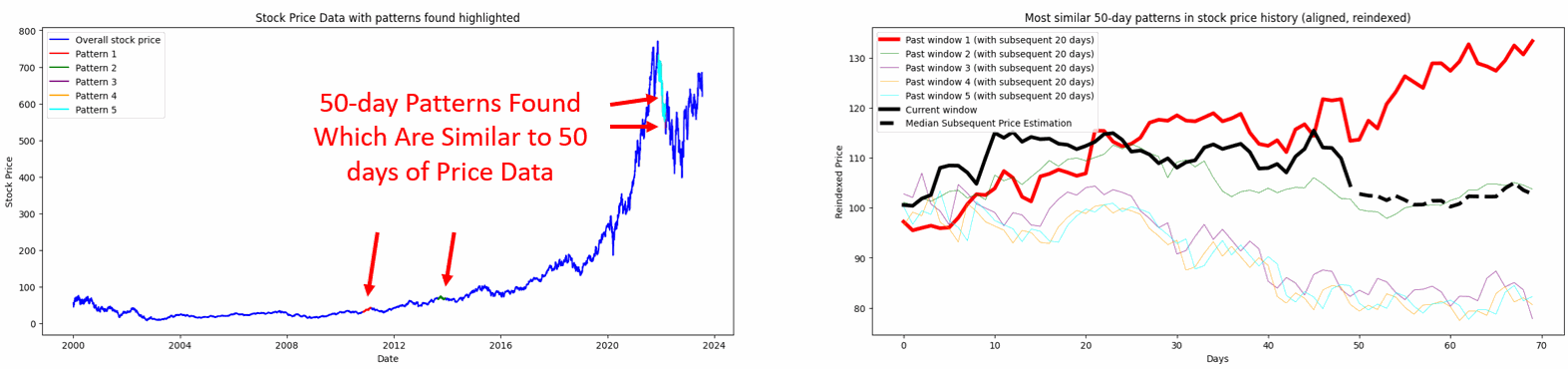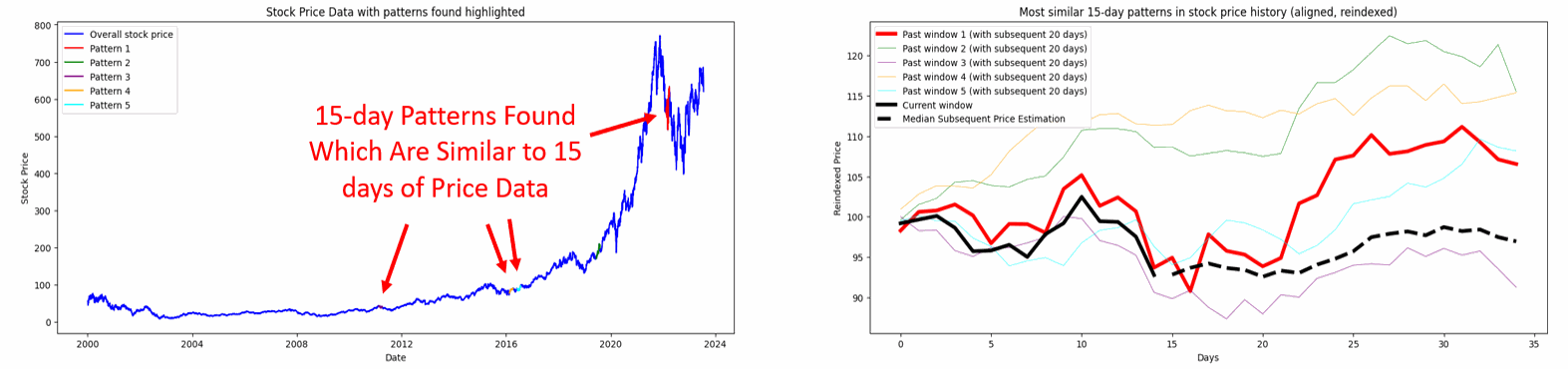
Figure 1. The method Pattern Recognition Method using PCA and DTW segments recent price data into a ‘current window’ and compares it to historical data windows of the same size, identifying and ranking the most similar patterns for different window sizes.
2. Implementation in Python
2.1 Importing Necessary Libraries
The libraries required include pandas, numpy, and matplotlib for data manipulation and visualization, yfinance for fetching stock price data, fastdtw for DTW implementation, scipy for distance computation, ta for technical analysis, sklearn for PCA and data imputation.
2.2 Adding Technical Indicators
Next, we define a function to compute and add various technical indicators to the stock price data. Technical indicators such as moving averages, Bollinger Bands, Ichimoku Cloud, etc., are included as demonstration and for the purpose of this article believed to be useful for understanding price movements. Any set of ‘explanatory’ variables can be included here.
def add_ta_features(data):
# function to add technical indicators
# ...
return data2.3 Data Normalization
Normalization is a crucial step to ensure that the data is on a similar scale. Define a function to normalize the time-series data.
def normalize(ts):
return (ts - ts.min()) / (ts.max() - ts.min())2.4 Dynamic Time Warping Distance Calculation
We then define a function to calculate the DTW distance, which incorporates the weighting scheme that balances the influence of price changes and technical indicators into the pattern recognition methodology.
Higher values would prioritize patterns closely aligned with price movements, while lower values would favor matches more reflective of the indicators used.
def dtw_distance(ts1, ts2, ts1_ta, ts2_ta, weight=0.75): # Adjust the weight parameter as needed
ts1_normalized = normalize(ts1)
ts2_normalized = normalize(ts2)
distance_pct_change, _ = fastdtw(ts1_normalized.reshape(-1, 1), ts2_normalized.reshape(-1, 1), dist=euclidean)
distance_ta, _ = fastdtw(ts1_ta, ts2_ta, dist=euclidean)
distance = weight * distance_pct_change + (1 - weight) * distance_ta
return distance2.5 Feature Reduction using PCA
Before employing DTW, we reduce the dimensionality of the technical indicator data using PCA with this function.
def extract_and_reduce_features(data, n_components=3):
ta_features = data.drop(columns=['Open', 'High', 'Low', 'Close', 'Volume', 'Adj Close'])
# Impute missing values
imputer = SimpleImputer(strategy='mean')
imputed_ta_features = imputer.fit_transform(ta_features)
pca = PCA(n_components=n_components)
reduced_features = pca.fit_transform(imputed_ta_features)
return reduced_features2.6 Fetching Data and Pre-processing
The next step is to fetch the stock price data, add technical indicators, reduce the features using PCA, and compute the percentage change in closing prices.
ticker = "ASML.AS"
start_date = '2000-01-01'
end_date = '2023-05-01'
data = yf.download(ticker, start=start_date, end=end_date)
data_with_ta = add_ta_features(data)
reduced_features = extract_and_reduce_features(data_with_ta, n_components=3)
price_data_pct_change = data_with_ta['Close'].pct_change().dropna()2.7 Complete Code
Stop Drowning In AI Information Overload
Your inbox is flooded with newsletters. Your feed is chaos. Somewhere in that noise are the insights that could transform your work—but who has time to find them?
The Deep View solves this. We read everything, analyze what matters, and deliver only the intelligence you need. No duplicate stories, no filler content, no wasted time. Just the essential AI developments that impact your industry, explained clearly and concisely.
Replace hours of scattered reading with five focused minutes. While others scramble to keep up, you'll stay ahead of developments that matter. 600,000+ professionals at top companies have already made this switch.
Finally, we amalgamate all of the above to implement the core logic to recognize similar patterns by 1) iterating through the data, 2) calculating DTW distances, 3) identifying the most similar patterns, and 4) visualizing the findings.
import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from fastdtw import fastdtw
from scipy.spatial.distance import euclidean
import ta
from sklearn.decomposition import PCA
from sklearn.impute import SimpleImputer
def add_ta_features(data):
# Add Trend indicators
data['trend_ichimoku_conv'] = ta.trend.ichimoku_a(data['High'], data['Low'])
data['trend_ema_slow'] = ta.trend.ema_indicator(data['Close'], 50)
data['momentum_kama'] = ta.momentum.kama(data['Close'])
data['trend_psar_up'] = ta.trend.psar_up(data['High'], data['Low'], data['Close'])
data['volume_vwap'] = ta.volume.VolumeWeightedAveragePrice(data['High'], data['Low'], data['Close'], data['Volume']).volume_weighted_average_price()
data['trend_ichimoku_a'] = ta.trend.ichimoku_a(data['High'], data['Low'])
data['volatility_kcl'] = ta.volatility.KeltnerChannel(data['High'], data['Low'], data['Close']).keltner_channel_lband()
data['trend_ichimoku_b'] = ta.trend.ichimoku_b(data['High'], data['Low'])
data['trend_ichimoku_base'] = ta.trend.ichimoku_base_line(data['High'], data['Low'])
data['trend_sma_fast'] = ta.trend.sma_indicator(data['Close'], 20)
data['volatility_dcm'] = ta.volatility.DonchianChannel(data['High'], data['Low'], data['Close']).donchian_channel_mband()
data['volatility_bbl'] = ta.volatility.BollingerBands(data['Close']).bollinger_lband()
data['volatility_bbm'] = ta.volatility.BollingerBands(data['Close']).bollinger_mavg()
data['volatility_kcc'] = ta.volatility.KeltnerChannel(data['High'], data['Low'], data['Close']).keltner_channel_mband()
data['volatility_kch'] = ta.volatility.KeltnerChannel(data['High'], data['Low'], data['Close']).keltner_channel_hband()
data['trend_sma_slow'] = ta.trend.sma_indicator(data['Close'], 200)
data['trend_ema_fast'] = ta.trend.ema_indicator(data['Close'], 20)
data['volatility_dch'] = ta.volatility.DonchianChannel(data['High'], data['Low'], data['Close']).donchian_channel_hband()
data['others_cr'] = ta.others.cumulative_return(data['Close'])
data['Adj Close'] = data['Close']
return data
def normalize(ts):
return (ts - ts.min()) / (ts.max() - ts.min())
def dtw_distance(ts1, ts2, ts1_ta, ts2_ta, weight=0.75): # Adjust the weight parameter as needed
ts1_normalized = normalize(ts1)
ts2_normalized = normalize(ts2)
distance_pct_change, _ = fastdtw(ts1_normalized.reshape(-1, 1), ts2_normalized.reshape(-1, 1), dist=euclidean)
distance_ta, _ = fastdtw(ts1_ta, ts2_ta, dist=euclidean)
distance = weight * distance_pct_change + (1 - weight) * distance_ta
return distance
def extract_and_reduce_features(data, n_components=3):
ta_features = data.drop(columns=['Open', 'High', 'Low', 'Close', 'Volume', 'Adj Close'])
# Impute missing values
imputer = SimpleImputer(strategy='mean')
imputed_ta_features = imputer.fit_transform(ta_features)
pca = PCA(n_components=n_components)
reduced_features = pca.fit_transform(imputed_ta_features)
return reduced_features
ticker = "ASML.AS"
start_date = '2000-01-01'
end_date = '2023-05-01'
data = yf.download(ticker, start=start_date, end=end_date)
data_with_ta = add_ta_features(data)
reduced_features = extract_and_reduce_features(data_with_ta, n_components=3)
price_data_pct_change = data_with_ta['Close'].pct_change().dropna()
subsequent_days = 15
days_to =[15, 20, 30]
min_gap = 10 # Set a minimum gap of 10 days between patterns found
for n_days in days_to:
current_window = price_data_pct_change[-n_days:].values
current_ta_window = reduced_features[-n_days:]
# Initialize distances with inf
distances = [np.inf] * (len(price_data_pct_change) - 2 * n_days - subsequent_days)
for start_index in range(len(price_data_pct_change) - 2 * n_days - subsequent_days):
# Ensure there is a minimum gap before or after the current window
gap_before = len(price_data_pct_change) - (start_index + n_days + subsequent_days)
gap_after = start_index - (len(price_data_pct_change) - n_days)
if gap_before >= min_gap or gap_after >= min_gap:
distances[start_index] = dtw_distance(
current_window,
price_data_pct_change[start_index:start_index + n_days].values,
current_ta_window,
reduced_features[start_index:start_index + n_days]
)
min_distance_indices = np.argsort(distances)[:3] # find indices of 3 smallest distances
fig, axs = plt.subplots(1, 2, figsize=(30, 8))
# plot the entire stock price data
axs[0].plot(data['Close'], color='blue', label='Overall stock price')
for i, start_index in enumerate(min_distance_indices):
# plot the pattern period in different colors
past_window_start_date = data.index[start_index]
past_window_end_date = data.index[start_index + n_days + subsequent_days]
axs[0].plot(data['Close'][past_window_start_date:past_window_end_date], color='C{}'.format(i), label=f"Pattern {i + 1}")
axs[0].set_title(f'{ticker} Stock Price Data')
axs[0].set_xlabel('Date')
axs[0].set_ylabel('Stock Price')
axs[0].legend()
# plot the reindexed patterns
for i, start_index in enumerate(min_distance_indices):
past_window = price_data_pct_change[start_index:start_index + n_days + subsequent_days]
reindexed_past_window = (past_window + 1).cumprod() * 100
axs[1].plot(range(n_days + subsequent_days), reindexed_past_window, color='C{}'.format(i), linewidth=3 if i == 0 else 1, label=f"Past window {i + 1} (with subsequent {subsequent_days} days)")
reindexed_current_window = (price_data_pct_change[-n_days:] + 1).cumprod() * 100
axs[1].plot(range(n_days), reindexed_current_window, color='k', linewidth=3, label="Current window")
# Collect the subsequent prices of the similar patterns
subsequent_prices = []
for i, start_index in enumerate(min_distance_indices):
subsequent_window = price_data_pct_change[start_index + n_days : start_index + n_days + subsequent_days].values
subsequent_prices.append(subsequent_window)
subsequent_prices = np.array(subsequent_prices)
median_subsequent_prices = np.median(subsequent_prices, axis=0)
# Adjusted line for reindexing the median subsequent prices
median_subsequent_prices_cum = (median_subsequent_prices + 1).cumprod() * reindexed_current_window.iloc[-1]
axs[1].plot(range(n_days, n_days + subsequent_days), median_subsequent_prices_cum, color='grey', linestyle='dashed', label="Median Subsequent Price Estimation")
axs[1].set_title(f"Most similar {n_days}-day patterns in {ticker} stock price history (aligned, reindexed)")
axs[1].set_xlabel("Days")
axs[1].set_ylabel("Reindexed Price")
axs[1].legend()
#plt.savefig(f'{ticker}_{n_days}_days.png')
#plt.close(fig)
plt.show()


Figure 2. Leveraging DTW and PCA, the visualization explores diverse window periods (15, 20, and 30 days) to identify and compare past pricing patterns in ASML.AS stock data with the most recent pattern. The plots, showcasing overall price data and reindexed, normalized patterns respectively, highlight three past instances that bear the closest resemblance in temporal dynamics.
3. Interpretation of Results
3.1 Top Patterns Identified
The core objective of this analysis is to leverage historical price patterns to understand possible future trajectories of the current stock price. We employed a combination of PCA and DTW to identify similar past price patterns in the stock data. The implemented code identifies and visualizes the top three patterns in the historical stock price data, ranking them from the most similar (Pattern 1) to the least similar (Pattern 3).
By comparing a recent price pattern with historical data, the code ranks the top three similar patterns from the past. These patterns are visualized alongside the recent pattern to provide a visual cue on how prices moved post those patterns. The code then estimates potential future prices based on a median price trajectory derived from these similar past patterns.
3.1 Accuracy of the Results
In the chart below, we explore the accuracy of all the patterns found in each window. The black line represents actual recent prices, while the colored lines depict the projected prices based on past patterns for different window sizes. Two dashed lines represent the median of the most similar projected prices (red) for each window, and the median of all projected prices (grey) across all patterns found, providing a consolidated view.
This visual representation serves as a compelling hypothesis on how the stock price might behave in the near future, derived from historical price behavior under similar market conditions. The overlapping, divergence, and direction of the actual prices with the projected median prices give a sense of the method’s potential and limitations in predicting price trajectories.

Figure 3. Actual vs Projected Prices: This graph contrasts reindexed actual prices with projections derived from historical patterns. The red dashed line represents the median of the projected prices from the most similar patterns, while the grey dashed line is the median of all projected prices, showcasing the method’s potential accuracy and range in predicting future price trajectories.
4. Limitations and Improvements
This has only been the first step in utilizing a combination of DTW and PCA for pattern recognition in stock price data. As a consequence, there are certain limitations and areas for improvement that should be considered.
4.1 Limitations
4.1.1. Optimization of Parameter through Backtesting
The performance of the DTW and PCA techniques significantly depends on the selection of parameters such as the weighting factor in the distance computation, the window sizes for days to window, and the variables chosen in PCA. Currently, there isn’t a systematic approach for parameter tuning.
Incorporating automated parameter tuning techniques like grid search or evolutionary algorithms could help in finding the optimal set of parameters that maximize the accuracy and reliability of the pattern recognition and projection methodology
4.1.2. Assumption of Repeating Patterns
The core assumption that past price patterns will reoccur in the future is a common simplification, yet it’s not always valid. Market dynamics evolve, and historical patterns may not necessarily repeat or lead to accurate projections.
4.2 Further Improvements
4.2.1. Incorporation of Additional Predictive Indicators
Extending the feature set by incorporating more diverse predictive indicators or alternative data sources could potentially enhance the accuracy of the pattern recognition methodology.
4.2.2. Statistical Validation of Patterns
An improvement could be making sure the patterns found are truly similar, not just by looking, but using a statistical test like a t-test. This test helps us see if the patterns we find in historical data are statistically similar to the current pattern or if they just look alike by chance.
4.2.3. Robustness Against Market Anomalies
Designing mechanisms to identify and adjust for price anomalies or extreme events could improve the resilience and accuracy of the pattern recognition and projection methodology. One way to smoothen out anomalies is through moving average methods.
4.2.4. Cross-Asset Pattern Recognition
Expanding the scope to include similar assets or even different markets could also provide a richer analysis. By looking at patterns across related assets or sectors, we might uncover broader market trends or recurring patterns that are not just limited to the individual asset initially analyzed.
5. Concluding Thoughts
We’ve taken some first steps towards a new way of finding patterns in stock prices. With DTW and PCA, we’ve started to sketch out a method that could help spot repeating patterns in historical stock data.
However, this is just a starting point. There are several areas we identified that need improvement, and the method needs to be tested more rigorously to see how well it really works.
Subscribe to our premium content to read the rest.
Become a paying subscriber to get access to this post and other subscriber-only content.
Upgrade







