
Trusted by millions. Actually enjoyed by them too.
Morning Brew makes business news something you’ll actually look forward to — which is why over 4 million people read it every day.
Sure, the Brew’s take on the news is witty and sharp. But the games? Addictive. You might come for the crosswords and quizzes, but you’ll leave knowing the stories shaping your career and life.
Try Morning Brew’s newsletter for free — and join millions who keep up with the news because they want to, not because they have to.
Elite Quant Plan – 14-Day Free Trial (This Week Only)
No card needed. Cancel anytime. Zero risk.
You get immediate access to:
Full code from every article (including today’s HMM notebook)
Private GitHub repos & templates
All premium deep dives (3–5 per month)
2 × 1-on-1 calls with me
One custom bot built/fixed for you
Try the entire Elite experience for 14 days — completely free.
→ Start your free trial now 👇
(Doors close in 7 days or when the post goes out of the spotlight — whichever comes first.)
See you on the inside.
👉 Upgrade Now →
🔔 Limited-Time Holiday Deal: 20% Off Our Complete 2026 Playbook! 🔔
Level up before the year ends!
AlgoEdge Insights: 30+ Python-Powered Trading Strategies – The Complete 2026 Playbook
30+ battle-tested algorithmic trading strategies from the AlgoEdge Insights newsletter – fully coded in Python, backtested, and ready to deploy. Your full arsenal for dominating 2026 markets.
Special Promo: Use code JANUARY2026 for 20% off
Valid only until January 25, 2026 — act fast!
👇 Buy Now & Save 👇
Instant access to every strategy we've shared, plus exclusive extras.
— AlgoEdge Insights Team
Premium Members – Your Full Notebook Is Ready
The complete Google Colab notebook from today’s article (with live data, full Hidden Markov Model, interactive charts, statistics, and one-click CSV export) is waiting for you.
Preview of what you’ll get:

Inside:
Interactive Distribution Plot with Specified Thresholds
Conditional Probabilities Over Time
Price Changes Thresholds Combinations
Beautiful interactive Plotly charts
Regime duration & performance tables
Ready-to-use CSV export
Free readers – you already got the full breakdown and visuals in the article. Paid members – you get the actual tool.
Not upgraded yet? Fix that in 10 seconds here👇
Google Collab Notebook With Full Code Is Available In the End Of The Article Behind The Paywall 👇 (For Paid Subs Only)
Conditional probability tells us how likely an event is after another event has already happened.
In asset price analysis, this can mean the chance of an extra price move, given a specific initial price move in a certain time.
In this article, we look at how to calculate the probability that a stock keeps moving in a given direction, based on a past move.
For example, if a stock drops 10% in one day, we might want the probability it drops another 5% the next day.
We walk through Python code for the analysis. You will also see references to an interactive Colab notebook.

We’ll discuss and implement the followinc concepts:
Interactive Distribution Plot with Specified Thresholds
Conditional Probabilities Over Time
Price Changes Thresholds Combinations
Dalio: “Stocks Only Look Strong in Dollar Terms.” Here’s a Globally Priced Alternative for Diversification.
Ray Dalio recently reported that much of the S&P 500’s 2025 gains came not from real growth, but from the dollar quietly losing value. Reportedly down 10% last year!
He’s not alone. Several BlackRock, Fidelity, and Bloomberg analysts say to expect further dollar decline in 2026.
So, even when your U.S. assets look “up,” your purchasing power may actually be down.
Which is why many investors are adding globally priced, scarce assets to their portfolios—like art.
Art is traded on a global stage, making it largely resistant to currency swings.
Now, Masterworks is opening access to invest in artworks featuring legends like Banksy, Basquiat, and Picasso as a low-correlation asset class with attractive appreciation historically (1995-2025).*
Masterworks’ 26 sales have yielded annualized net returns like 14.6%, 17.6%, and 17.8%.
They handle the sourcing, storage, and sale. You just click to invest.
Special offer for my subscribers:
*Based on Masterworks data. Investing involves risk. Past performance is not indicative of future returns. Important Reg A disclosures: masterworks.com/cd.
1. Understanding Conditional Probabilities
Conditional probability measures the likelihood of Event A, assuming Event B has occurred. Mathematically:

Where:
P(A∩B) is the probability of both events A and B occurring.
P(B) is the probability of event B occurring.
In stock price terms, we might want P(large drop in the next week ∣ big jump today).
1.1 Use Cases in Price Analysis
Trend Confirmation: Traders might look at the probability of another price increase, given an initial jump. If stock X rises 10% today, we can check the chance of a further 5% gain soon.
Risk Management: We can estimate the probability of a big drop happening after a rise. If a stock surged 6% yesterday, you could gauge the odds of an 8% drop in the next two days.
Pattern Recognition: Some stocks show recurring short-term patterns. For instance, you might see a 5% rise soon after a 3% drop. Conditional probability puts a number on how often that pattern repeats.
Event-Driven Strategies: You can measure the probability of a price drop after an earnings report. This helps traders plan trades around big announcements.
1.2 Institutional Investors
Large funds often monitor how certain price moves tend to lead to other moves.
They might spot that after a 10% rise in a technology stock, a 3% pullback frequently follows in the next three days.
1.3 High-Frequency Trading
HFT firms also rely on conditional probabilities. Their algorithms look for rapid signals.
For example, when trading volume spikes, the algorithm might check how often that leads to a quick price jump, then place trades accordingly.
2. Conditional Probabilities in Python
Below is an example of interactive code that calculates and plots these probabilities.
We use historical data for ASML (a major European semiconductor company).
If You Could Be Earlier Than 85% of the Market?
Most read the move after it runs. The top 250K start before the bell.
Elite Trade Club turns noise into a five-minute plan—what’s moving, why it matters, and the stocks to watch now. Miss it and you chase.
Catch it and you decide.
By joining, you’ll receive Elite Trade Club emails and select partner insights. See Privacy Policy.
2.1 Interactive Distribution Plot
We define parameters for the first and second move and set thresholds for each. For instance:
first_move_days = 1second_move_days = 2first_threshold_percentage = 0.06(6%)second_threshold_percentage = 0.08(8%)
This checks: “What is the probability of an 8% move in two days if we already had a 6% move in one day?”
import yfinance as yf
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from ipywidgets import interact, widgets
import matplotlib.colors as mcolors
symbol = "ASML.AS"
data = yf.download(symbol, start='2000-01-01', end='2025-12-02')
initial_first_move_days = 1
initial_second_move_days = 2
initial_first_threshold_percentage = 0.06 # 6%
initial_second_threshold_percentage = 0.08 # 8%def conditional_probability_analysis(first_move_days, second_move_days, first_threshold_percentage, second_threshold_percentage):
# Calculate the first move percentage change
data[f'{first_move_days}d_pct_change_first'] = data['Adj Close'].pct_change(first_move_days)
# Calculate the second move percentage change only if the first move change is above threshold
data.loc[data[f'{first_move_days}d_pct_change_first'].abs() >= first_threshold_percentage, f'{second_move_days}d_pct_change_second'] = data['Adj Close'].shift(-second_move_days).pct_change(second_move_days)
# Calculate the frequency of the conditional threshold percentage change (increase or decrease) for the second move
total_periods = len(data)
down_periods = len(data[data[f'{second_move_days}d_pct_change_second'] <= -second_threshold_percentage])
up_periods = len(data[data[f'{second_move_days}d_pct_change_second'] >= second_threshold_percentage])
down_frequency = down_periods / total_periods
up_frequency = up_periods / total_periods
# Plotting
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(24, 8))
sns.histplot(data=data, x=f'{second_move_days}d_pct_change_second', kde=True, bins=100, ax=ax1)
ax1.axvline(x=-second_threshold_percentage, color='r', linestyle='--', label=f"Probability of {second_move_days}-day {second_threshold_percentage * 100:.2f}% decrease after a {first_move_days}-day {first_threshold_percentage * 100:.2f}% change: {down_frequency * 100:.2f}%")
ax1.axvline(x=second_threshold_percentage, color='b', linestyle='--', label=f"Probability of {second_move_days}-day {second_threshold_percentage * 100:.2f}% increase after {first_move_days}-day {first_threshold_percentage * 100:.2f}% change: {up_frequency * 100:.2f}%")
ax1.legend()
ax1.set_xlabel('Percentage change')
ax1.set_ylabel('Frequency')
ax1.set_title(f'Distribution of {second_move_days}-day {second_threshold_percentage * 100:.2f}% changes for {symbol} after a {first_move_days}-day {first_threshold_percentage * 100:.2f}% change')
# Plot the stock price
data['Adj Close'].plot(ax=ax2)
up_instances = data[data[f'{second_move_days}d_pct_change_second'] >= second_threshold_percentage]
down_instances = data[data[f'{second_move_days}d_pct_change_second'] <= -second_threshold_percentage]
ax2.scatter(up_instances.index, up_instances['Adj Close'], color='b', marker='^', label=f"{second_move_days}-day {second_threshold_percentage * 100:.2f}% increase after {first_move_days}-day {first_threshold_percentage * 100:.2f}% change")
ax2.scatter(down_instances.index, down_instances['Adj Close'], color='r', marker='v', label=f"{second_move_days}-day {second_threshold_percentage * 100:.2f}% decrease after {first_move_days}-day {first_threshold_percentage * 100:.2f}% change")
ax2.legend()
ax2.set_xlabel('Date')
ax2.set_ylabel('Adjusted Close Price')
ax2.set_title(f'Stock Price for {symbol} with {second_move_days}-day {second_threshold_percentage * 100:.2f}% changes after a {first_move_days}-day {first_threshold_percentage * 100:.2f}% change markers')
plt.tight_layout()
plt.show()
# Creating sliders for interactive inputs with initialized values
first_move_days_slider = widgets.IntSlider(min=1, max=30, step=1, value=initial_first_move_days, description="First Move Days")
second_move_days_slider = widgets.IntSlider(min=1, max=30, step=1, value=initial_second_move_days, description="Second Move Days")
first_threshold_percentage_slider = widgets.FloatSlider(min=0.01, max=0.5, step=0.001, value=initial_first_threshold_percentage, description="First Threshold %")
second_threshold_percentage_slider = widgets.FloatSlider(min=0.01, max=0.5, step=0.001, value=initial_second_threshold_percentage, description="Second Threshold %")
# Use interact function with conditional_probability_analysis function and the sliders
interact(conditional_probability_analysis,
first_move_days=first_move_days_slider,
second_move_days=second_move_days_slider,
first_threshold_percentage=first_threshold_percentage_slider,
second_threshold_percentage=second_threshold_percentage_slider);
Figure. 1: The top plot shows the distribution of two-day, 8% price changes following a one-day, 6% price move. The lower plot shows the adjusted close price with markers for each time such large two-day changes occurred after that prior move.
Results Interpretation
The histogram often centers near 0% for the two-day change after a 6% rise. That suggests the stock tends to stabilize rather than keep moving sharply up or down.
We might see something like 0.33% probability of an 8% drop, which is quite low, and 0.60% probability of an 8% rise, which is also low.
The few blue or red markers on the chart indicate how rare these big moves are after the initial 6% jump.
Practical Insights
Stabilization: A 6% one-day gain often does not lead to a further major shift.
Risk of Holding: A large drop after that kind of gain is not common, based on the data.
Limited Upside: A further 8% gain is possible but still not frequent.
Rare Large Movements: Either big increase or drop in the following days is unusual.
2.2 Conditional Probability Over Time
You can repeat this analysis over rolling windows of different sizes (for example, 126, 252, 504 days). This reveals how these probabilities shift across time and where they are more likely to occur
In the provided plot, we analyze the conditional probabilities of 2-day 8.00% price movements given a 1-day 6.00% change, using rolling windows of 126 days (~6 months), 252 days (1 year), and 504 days (2 years).
# Rolling window analysis with different window sizes
rolling_windows = [126, 252, 504] # 6 months, 1 year, and 2 years
# Generate color shades
def get_shade(base_color, factor):
return tuple(min(1, base + factor) for base in base_color)
base_red = (1, 0, 0)
base_blue = (0, 0, 1)
colors_down = [mcolors.to_hex(get_shade(base_red, i * 0.2)) for i in range(len(rolling_windows))]
colors_up = [mcolors.to_hex(get_shade(base_blue, i * 0.2)) for i in range(len(rolling_windows))]
# Plot rolling window analysis for up and down movements
fig, ax3 = plt.subplots(figsize=(24, 8))
for i, window in enumerate(rolling_windows):
rolling_down = data['Adj Close'].rolling(window=window).apply(
lambda x: np.mean((x.pct_change(initial_first_move_days).abs() >= initial_first_threshold_percentage) &
(x.pct_change(initial_second_move_days).shift(-initial_second_move_days) <= -initial_second_threshold_percentage))
)
rolling_up = data['Adj Close'].rolling(window=window).apply(
lambda x: np.mean((x.pct_change(initial_first_move_days).abs() >= initial_first_threshold_percentage) &
(x.pct_change(initial_second_move_days).shift(-initial_second_move_days) >= initial_second_threshold_percentage))
)
ax3.plot(rolling_down, label=f'Down Movements (Window: {window} days)', color=colors_down[i])
ax3.plot(rolling_up, label=f'Up Movements (Window: {window} days)', color=colors_up[i])
ax3.set_xlabel('Date')
ax3.set_ylabel('Conditional Probability')
ax3.set_title(f'Rolling Window Analysis of {initial_second_move_days}-day {initial_second_threshold_percentage * 100:.2f}% Conditional Price Movements conditional on {initial_first_move_days}-day {initial_first_threshold_percentage * 100:.2f}% change')
ax3.legend()
ax3.grid(True)
plt.tight_layout()
plt.show()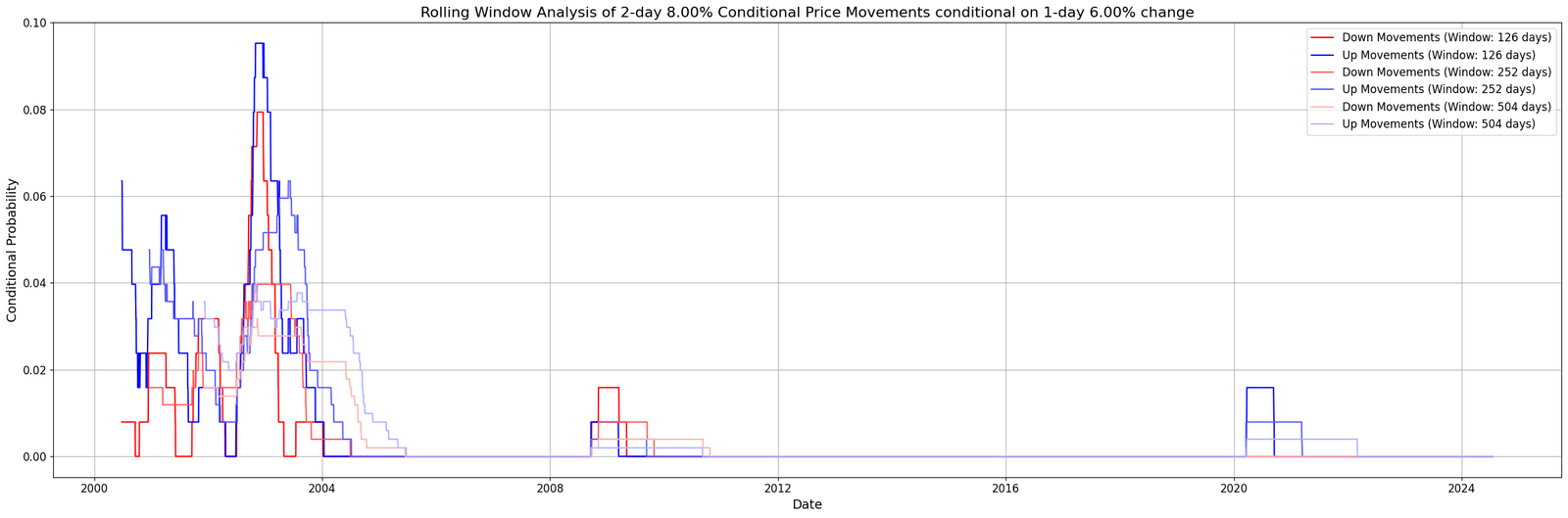
Figure. 2: Shows the changing probabilities for two-day, 8% moves after a one-day, 6% move, using different rolling windows.
Results Interpretation
Blue Lines (Up Moves): Probability of a further up move after an initial up.
Red Lines (Down Moves): Probability of a down move after an initial up.
High Volatility Periods: In earlier years (e.g., early 2000s), these probabilities spike, suggesting more extreme moves.
Later Stability: In more recent years, spikes are lower, which implies fewer large swings.
Short vs. Long-Term Windows: A 126-day window is noisier, while 252-day or 504-day windows reveal broader trends.
2.3 Conditional Probability Across Thresholds
We can also visualize how these probabilities change for various threshold levels.
The code below produces heatmaps for different threshold pairs and includes 30-day volatility in parentheses for further context.
Absolute Movements — conditional probabilities regardless of the direction (up or down)
Down-Down Movements — For down-down movements, the heatmap indicates how likely it is for a price drop to be followed by another price drop.
Up-Down Movements — For down-down movements, the heatmap indicates how likely it is for a price drop to be followed by another price drop.
Up-Down Movements — This combination shows the likelihood of a price increase followed by a price decrease.
Down-Up Movements — Conversely, this combination highlights the probability of a price drop being followed by a price increase.
# Percentage thresholds
thresholds = np.linspace(0.01, 0.15, 11) # Thresholds from 1% to 15%
# Calculate rolling volatility (30-day)
data['30d_volatility'] = data['Adj Close'].pct_change().rolling(window=30).std()
# Initialize matrices for different scenarios
prob_matrix = np.zeros((len(thresholds), len(thresholds)), dtype=object)
prob_matrix_downs = np.zeros((len(thresholds), len(thresholds)), dtype=object)
prob_matrix_ups = np.zeros((len(thresholds), len(thresholds)), dtype=object)
prob_matrix_up_after_down = np.zeros((len(thresholds), len(thresholds)), dtype=object)
prob_matrix_down_after_up = np.zeros((len(thresholds), len(thresholds)), dtype=object)
# Calculate conditional probabilities and volatilities for each scenario
for i, first_threshold in enumerate(thresholds):
for j, second_threshold in enumerate(thresholds):
first_condition = data['Adj Close'].pct_change(initial_first_move_days).abs() >= first_threshold
second_condition = data['Adj Close'].shift(-initial_second_move_days).pct_change(initial_second_move_days).abs() >= second_threshold
combined_condition = first_condition & second_condition
prob_matrix[i, j] = (
np.mean(combined_condition),
np.mean(data['30d_volatility'][combined_condition])
)
# Only downs
first_condition_down = data['Adj Close'].pct_change(initial_first_move_days) <= -first_threshold
second_condition_down = data['Adj Close'].shift(-initial_second_move_days).pct_change(initial_second_move_days) <= -second_threshold
combined_condition_downs = first_condition_down & second_condition_down
prob_matrix_downs[i, j] = (
np.mean(combined_condition_downs),
np.mean(data['30d_volatility'][combined_condition_downs])
)
# Only ups
first_condition_up = data['Adj Close'].pct_change(initial_first_move_days) >= first_threshold
second_condition_up = data['Adj Close'].shift(-initial_second_move_days).pct_change(initial_second_move_days) >= second_threshold
combined_condition_ups = first_condition_up & second_condition_up
prob_matrix_ups[i, j] = (
np.mean(combined_condition_ups),
np.mean(data['30d_volatility'][combined_condition_ups])
)
# Up after down
second_condition_up_after_down = data['Adj Close'].shift(-initial_second_move_days).pct_change(initial_second_move_days) >= second_threshold
combined_condition_up_after_down = first_condition_down & second_condition_up_after_down
prob_matrix_up_after_down[i, j] = (
np.mean(combined_condition_up_after_down),
np.mean(data['30d_volatility'][combined_condition_up_after_down])
)
# Down after up
second_condition_down_after_up = data['Adj Close'].shift(-initial_second_move_days).pct_change(initial_second_move_days) <= -second_threshold
combined_condition_down_after_up = first_condition_up & second_condition_down_after_up
prob_matrix_down_after_up[i, j] = (
np.mean(combined_condition_down_after_up),
np.mean(data['30d_volatility'][combined_condition_down_after_up])
)
# Helper function to format the annotations
def format_annotation(value):
return f"{value[0]:.3f}\n({value[1]:.3f})" if value[0] > 0 else "N/A"
# Create annotation matrices
annot_matrix = np.vectorize(format_annotation)(prob_matrix)
annot_matrix_downs = np.vectorize(format_annotation)(prob_matrix_downs)
annot_matrix_ups = np.vectorize(format_annotation)(prob_matrix_ups)
annot_matrix_up_after_down = np.vectorize(format_annotation)(prob_matrix_up_after_down)
annot_matrix_down_after_up = np.vectorize(format_annotation)(prob_matrix_down_after_up)
# Plot heatmaps for each scenario
plt.figure(figsize=(12, 6))
sns.heatmap(np.array([[v[0] for v in row] for row in prob_matrix]), xticklabels=np.round(thresholds, 2), yticklabels=np.round(thresholds, 2), cmap='coolwarm', annot=annot_matrix, fmt="", cbar_kws={'label': 'Conditional Probability'})
plt.xlabel(f'Second Move Threshold')
plt.ylabel(f'First Move Threshold')
plt.title(f'Conditional Probabilities of {initial_second_move_days}-day Absolute Price Movements for {symbol}\nconditional on {initial_first_move_days}-day Absolute Movements (30d Volatility in Parentheses)')
plt.show()
plt.figure(figsize=(12, 6))
sns.heatmap(np.array([[v[0] for v in row] for row in prob_matrix_downs]), xticklabels=np.round(thresholds, 2), yticklabels=np.round(thresholds, 2), cmap='coolwarm', annot=annot_matrix_downs, fmt="", cbar_kws={'label': 'Conditional Probability'})
plt.xlabel(f'Second Move Down Threshold')
plt.ylabel(f'First Move Down Threshold')
plt.title(f'Conditional Probabilities of {initial_second_move_days}-day Down Price Movements for {symbol}\nconditional on {initial_first_move_days}-day Down Movements (30d Volatility in Parentheses)')
plt.show()
plt.figure(figsize=(12, 6))
sns.heatmap(np.array([[v[0] for v in row] for row in prob_matrix_ups]), xticklabels=np.round(thresholds, 2), yticklabels=np.round(thresholds, 2), cmap='coolwarm', annot=annot_matrix_ups, fmt="", cbar_kws={'label': 'Conditional Probability'})
plt.xlabel(f'Second Move Up Threshold')
plt.ylabel(f'First Move Up Threshold')
plt.title(f'Conditional Probabilities of {initial_second_move_days}-day Up Price Movements for {symbol}\nconditional on {initial_first_move_days}-day Up Movements (30d Volatility in Parentheses)')
plt.show()
plt.figure(figsize=(12, 6))
sns.heatmap(np.array([[v[0] for v in row] for row in prob_matrix_up_after_down]), xticklabels=np.round(thresholds, 2), yticklabels=np.round(thresholds, 2), cmap='coolwarm', annot=annot_matrix_up_after_down, fmt="", cbar_kws={'label': 'Conditional Probability'})
plt.xlabel(f'Second Move Up Threshold')
plt.ylabel(f'First Move Down Threshold')
plt.title(f'Conditional Probabilities of {initial_second_move_days}-day Up Price Movements for {symbol}\nconditional on {initial_first_move_days}-day Down Movements (30d Volatility in Parentheses)')
plt.show()
plt.figure(figsize=(12, 6))
sns.heatmap(np.array([[v[0] for v in row] for row in prob_matrix_down_after_up]), xticklabels=np.round(thresholds, 2), yticklabels=np.round(thresholds, 2), cmap='coolwarm', annot=annot_matrix_down_after_up, fmt="", cbar_kws={'label': 'Conditional Probability'})
plt.xlabel(f'Second Move Down Threshold')
plt.ylabel(f'First Move Up Threshold')
plt.title(f'Conditional Probabilities of {initial_second_move_days}-day Down Price Movements for {symbol}\nconditional on {initial_first_move_days}-day Up Movements (30d Volatility in Parentheses)')
plt.show()

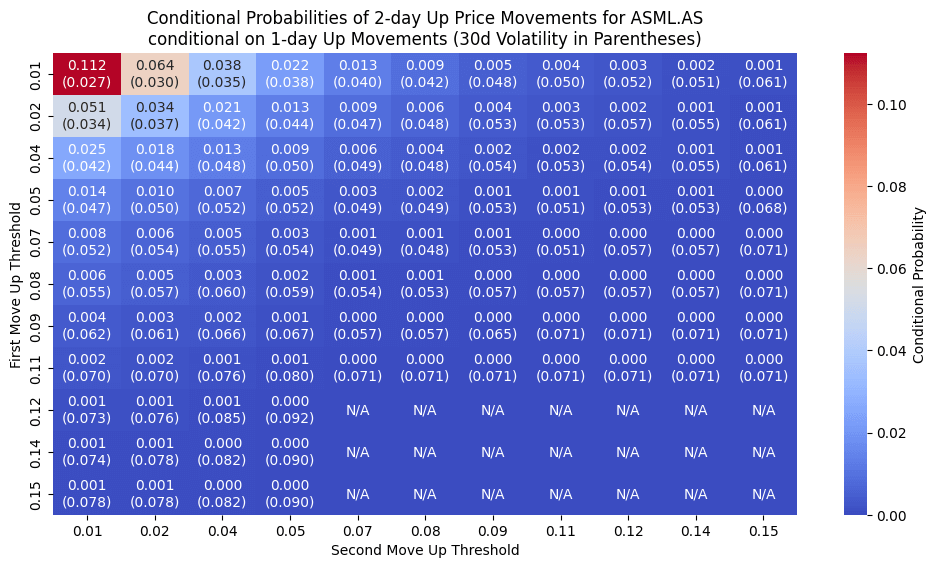
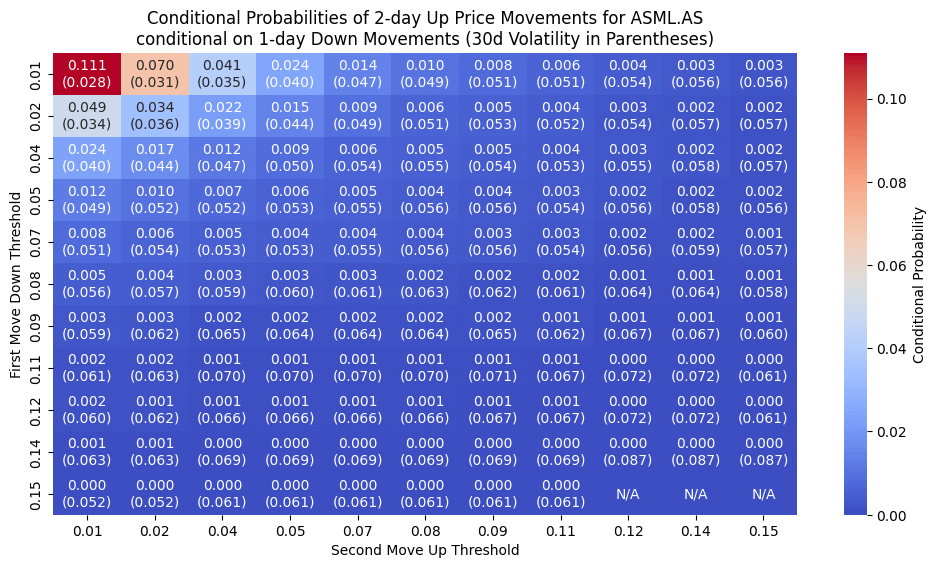

Figure. 3: A dancer’s movement captured through the Ego-Exo4D lens, accompanied by expert commentary, showcases the dataset’s depth in analyzing the finesse of human skill.
Example: Top-Left Cell
If both thresholds are 1%, you might see something like a 42% chance that the stock moves at least 1% over two days, given that it already moved 1% in the prior day. Meanwhile, the 30-day volatility might be around 2.8%.
Practical Insights
High-Probability Zones: Smaller moves tend to be followed by smaller subsequent moves, which can inform tight stops.
Trend Continuation vs. Reversal: Heatmaps for up-up or down-down patterns show whether the stock typically follows a current direction or snaps back.
Volatility Context: If high probability coincides with high volatility, you might expect big swings.
3. Limitations and Improvements
3.1 Limitations
Historical Dependence: This relies on past data and might fail if market conditions shift abruptly.
Simplistic Independence Assumption: External factors like news, macro data, or market sentiment can affect prices but aren’t included here.
Overfitting: When samples are small, these probabilities might not generalize to future data.
Limited Scope: The approach focuses on percentage changes. Including volume or economic events might improve accuracy.
3.2 Improvements
Incorporating More Variables: Including additional variables such as trading volume, sector performance, and macroeconomic indicators can provide a more view of stock price movements.
Machine Learning Techniques: Algorithms like random forests be trained to estimate future price movements conditional on how it moved n-days prior.
Concluding Thoughts
Conditional probability adds a statistical lens to trading decisions. It can show how large or small a follow-up move might be, given a prior change.
Still, real markets can shift due to broad external factors, so treat these results with caution.
Subscribe to our premium content to read the rest.
Become a paying subscriber to get access to this post and other subscriber-only content.
Upgrade







